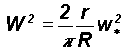
Signatures of quantum-like chaos in spacing intervals of non-trivial Riemann zeta zeros and in turbulent fluid flows

A.M.Selvam

Indian Institute of Tropical Meteorology, Pune 411 008, India

(Retired) email: selvam@ip.eth.net
website: http://www.geocities.com/amselvam
 
 
 

Abstract

    The spacing intervals of adjacent Riemann zeta zeros(non-trivial) exhibit fractal(irregular) fluctuations generic to dynamical systems in nature such as fluid flows, heart beat patterns, stock market price index, etc., and are associated with unpredictability or chaos. The power spectra of such fractal space-time fluctuations exhibit universal inverse power law form and signify long-range correlations, identified as self-organized criticality . A cell dynamical system model developed by the author for turbulent fluid flows provides a unique quantification for the observed power spectra in terms of the statistical normal distribution, such that the variance represents the statistical probability densities. Such a result that the additive amplitudes of eddies  when squared, represent the statistical probabilities is an observed feature of the subatomic dynamics of quantum systems such as an electron or photon. Self-organized criticality is therefore a signature of quantum-like chaos in dynamical systems. The model concepts are applicable to all real world(observed) and computed(mathematical model) dynamical systems.
    Continuous periodogram analyses of the fractal fluctuations of Riemann zeta zero spacing intervals show that the power spectra follow the unique and universal inverse power law form of the statistical normal distribution. The Riemann zeta zeros therefore exhibit quantum-like chaos, the spacing intervals of the zeros representing  the energy(variance) level spacings of quantum-like chaos inherent to dynamical systems in nature. The cell dynamical system model is a general systems theory applicable to dynamical systems of all size scales.

1.    Introduction

    Riemann zeta function z(s) is a function of the complex variable s and is defined as a sum over all integers( Keating, 1990)

z(s) = 1+1/2s +1/3s +1/4s +1/5s + ......... if x > 1.

(1)


The analytic properties of the zeta function are also related to the distribution of prime numbers. It is known that there are an infinite number of prime numbers. Though the prime numbers appear to be distributed at random among the integers, the distribution follows the approximate law that the number of primes p(x) upto the integer x is equal to x/logx  where log is the natural logarithm.The actual distribution of primes fluctuate on either side of the estimated value and approach closely the estimated value for large values of x.
    In 1859 Bernhard Riemann gave an exact formula for the counting function p(x) , in which fluctuations about the average are related to the value of s for which z(s) =0 , s being a complex number. Based on a few numerical computations Riemann conjectured that an important set of the zeros, namely the non-trivial zeros, all have real part equal to x = 1/2 . This is the Riemann hypothesis(Keating,1990; Devlin,1997). Numerical computations done so far agree with Riemann's hypothesis. However, a theoretical proof will establish the validity of numerous results in number theory which assume that the Riemann hypothesis is true.
    A proof of Riemann hypothesis will also help physicists to compute the chaotic orbits of complex atomic systems such as a hydrogen atom in a magnetic field, to the oscillations of large nuclei (Richards, 1988; Gutzwiller, 1990; Berry, 1992; Cipra, 1996; Klarreich, 2000). It is now believed that the spectrum of Riemann zeta zeros represent the energy spectrum of complex quantum systems which exhibit classical chaos.
    A cell dynamical system model developed by the author shows that quantum-like chaos is inherent to fractal space-time fluctuations exhibited by dynamical systems in nature ranging from subatomic and molecular scale quantum systems to macroscale turbulent fluid flows. The model provides a unique quantification for the fractal fluctuations in terms of the statistical normal distribution. The Riemann zero spacing intervals exhibit fractal fluctuations and the power spectrum exhibits model predicted universal inverse power law form of the statistical normal distribution. The distribution of Riemann zeros therefore exhibit quantum-like chaos.

2.    Cell dynamical system model

    As mentioned earlier(Section 1: Introduction) power spectral analyses of fractal space-time fluctuations exhibits inverse power law form, i.e., a selfsimilar eddy continuum. The cell dynamical system model (Mary Selvam, 1990; Selvam and Fadnavis, 1998, and all references contained therein) is a general systems theory (Capra, 1996) applicable to dynamical systems of all size scales. The model shows that such an eddy continuum can be visualised as a hierarchy of successively larger scale eddies enclosing smaller scale eddies. Eddy or wave is characterised by circulation speed and radius. Large eddies of root mean square(r.m.s) circulation speed W and radius R  form as envelopes enclosing small eddies of r.m.s circulation speed w*  and radius r  such that

(2)


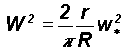
Large eddies are visualised to grow at unit length step increments at unit intervals of time, the units for length and time scale increments being respectively equal to the enclosed small eddy perturbation length scale r and the eddy circulation time scale t .
    Since the large eddy is but the average of the enclosed smaller eddies, the eddy energy spectrum follows the statistical normal distribution according to the Central Limit Theorm (Ruhla, 1992). Therefore, the variance represents the probability densities. Such a result that the additive amplitudes of the eddies, when squared, represent the probabilities is an observed feature of the subatomic dynamics of quantum systems such as the electron or photon (Maddox 1988a, 1993; Rae, 1988 ). The fractal space-time fluctuations exhibited by dynamical systems are signatures of quantum-like mechanics. The cell dynamical system model provides a unique quantification for the apparently chaotic or unpredictable nature of such fractal fluctuations ( Selvam and Fadnavis, 1998). The model predictions for quantum-like chaos of dynamical systems are as follows.

(a) The observed fractal fluctuations of dynamical systems are generated by an overall logarithmic spiral trajectory with the quasiperiodic Penrose tiling pattern for the internal structure.

(b) Conventional continuous periodogram power spectral analyses of such spiral trajectories will reveal a continuum of periodicities with progressive increase in phase.

(c) The broadband power spectrum will have embedded dominant wave-bands, the bandwidth increasing with period length. The peak periods(or length scales) En in the dominant wavebands will be given by the relation

En=TS(2+t )t n

(3)


where t is the golden mean equal to (1+Ö 5)/2 [@ 1.618] and Ts , the primary perturbation length scale. Considering the most representative example of turbulent fluid flows, namely, atmospheric flows, Ghil(1994) reports that the most striking feature in climate variability on all time scales is the presence of sharp peaks superimposed on a continuous background.

The model predicted periodicities(or length scales) in terms of the primary perturbation length scale units are are 2.2, 3.6, 5.8, 9.5, 15.3, 24.8, 40.1,and 64.9 respectively for values of n ranging from -1 to 6. Peridicities close to model predicted have been reported in weather and climate variability (Burroughs 1992; Kane 1996).

(d) The ratio r/R also represents the increment dq  in phase angle q (Equation 2 ).  Therefore the phase angle q represents the variance. Hence, when the logarithmic spiral is resolved as an eddy continuum in conventional spectral analysis, the increment in wavelength is concomitant with increase in phase (Selvam and Fadnavis, 1998). Such a result that increments in wavelength and phase angle are related is observed in quantum systems and has been named 'Berry's phase' (Berry 1988; Maddox 1988b; Simon et al., 1988; Anandan, 1992). The relationship of angular turning of the spiral to intensity of fluctuations is seen in the tight coiling of the hurricane spiral cloud systems.

The overall logarithmic spiral flow structure is given by the relation

(4)


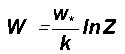
where the constant k is the steady state fractional volume dilution of large eddy by inherent turbulent eddy fluctuations . The constant k is equal to 1/t2(@0.382) and is identified as the universal constant for deterministic chaos in fluid flows (Selvam and Fadnavis, 1998).The steady state emergence of fractal structures is therefore equal to

1/k @ 2.62

(5)


The model predicted logarithmic wind profile relationship such as Equation 4 is a long-established(observational) feature of atmospheric flows in the boundary layer,the constant k, called the Von Karman ’s constant has the value equal to 0.38 as determined from observations ( Hogstrom, 1985).

In Equation 4, W represents the standard deviation of eddy fluctuations, since W is computed as the instantaneous r.m.s. ( root mean square) eddy perturbation amplitude with reference to the earlier step of eddy growth. For two successive stages of eddy growth starting from primary perturbation w*the ratio of the standard deviations Wn+1 and Wn is given from Equation 4 as (n+1)/n. Denoting by s the standard deviation of eddy fluctuations at the reference level (n=1) , the standard deviations of eddy fluctuations for successive stages of eddy growth are given as integer multiple of s , i.e., s , 2s , 3s , etc. and correspond respectively to

statistical normalized standard deviation t=0,1,2,3, etc.

(6)


The conventional power spectrum plotted as the variance versus the frequency in log-log scale will now represent the eddy probability density on logarithmic scale versus the standard deviation of the eddy fluctuations on linear scale since the logarithm of the eddy wavelength represents the standard deviation i.e., the r.m.s. value of eddy fluctuations (Equation 4). The r.m.s. value of eddy fluctuations can be represented in terms of statistical normal distribution as follows. A normalized standard deviation t=0 corresponds to cumulative percentage probability density equal to 50 for the mean value of the distribution. Since the logarithm of the wavelength represents the r.m.s. value of eddy fluctuations the normalized standard deviation t is defined for the eddy energy as

(7)


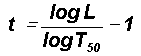
where L is the period in years and T50 is the period up to which the cumulative percentage contribution to total variance is equal to 50 and t = 0. The variable LogT50 also represents the mean value for the r.m.s. eddy fluctuations and is consistent with the concept of the mean level represented by r.m.s. eddy fluctuations. Spectra of time series of fluctuations of dynamical systems, for example, meteorological parameters, when plotted as cumulative percentage contribution to total variance versus t should follow the model predicted universal spectrum (Selvam and Fadnavis, 1998, and all  references therein). The literature shows many examples of pressure, wind and temperature whose shapes display a remarkable degree of universality(Canavero and Einaudi,1987).

The periodicities(or length scales) T50 and T95 up to which the cumulative percentage contribution to total variances are respectively equal to 50 and 95 are computed from model concepts as follows.

The power spectrum, when plotted as normalised standard deviation t versus cumulative percentage contribution to total variance represents the statistical normal distribution (Equation 7), i.e., the variance represents the probability density. The normalised standard deviation values t corresponding to cumulative percentage probability densities P equal to 50 and 95 respectively are equal to 0 and 2 from statistical normal distribution characteristics. Since t represents the eddy growth step n (Equation 6) the dominant periodicities(or length scales) T50 and T95 upto which the cumulative percentage contribution to total variance are respectively equal to 50 and 95 are obtained from Equation 3 for corresponding values of n equal to 0 and 2. In the present study of fractal fluctuations of spacing intervals of adjacent Riemann zeta zeros, the primary perturbation length scale Ts is equal to unit spacing interval and T50 and T95 are obtained as

T50 = (2+t )t0 @ 3.6 unit spacing intervals

(8)
T95 = (2+t )t2 @ 9.5 unit spacing intervals
(9)


3.    Data and Analysis

    Details of the Riemann zeta zeros(non-trivial) used in the present study are given in the following:
(a)     The first 100000 zeros were obtained from:
http://www.research.att.com/~amo/zeta_tables/zeros1

(b)    Riemann zeta zeros numbered 10^12 + 1 through 10^12 + 10^4 were obtained from:
http://www.research.att.com/~amo/zeta_tables/zeros3
[ Values of gamma - 267653395647, where gamma runs over the heights of the
zeros of the Riemann zeta numbered 10^12 + 1 through 10^12 + 10^4. Thus
zero # 10^12 + 1 is actually
1/2 + i * 267,653,395,648.8475231278...
Values are guaranteed to be accurate only to within 10^(-8) ].

(c)     Riemann zeta zeros numbered 10^21 + 1 through 10^21 + 10^4 were obtained from:
http://www.research.att.com/~amo/zeta_tables/zeros4
[ Values of gamma - 144176897509546973000, where gamma runs over the heights
of the zeros of the Riemann zeta numbered 10^21 + 1 through 10^21 + 10^4.
Thus zero # 10^21 + 1 is actually
1/2 + i * 144,176,897,509,546,973,538.49806962...
Values are not guaranteed, and are probably accurate to within 10^(-6) ].

(d)    Riemann zeta zeros numbered 10^22 + 1 through 10^22 + 10^4 were obtained from:
http://www.research.att.com/~amo/zeta_tables/zeros5
[ Values of gamma - 1370919909931995300000, where gamma runs over the heights
of the zeros of the Riemann zeta numbered 10^22 + 1 through 10^22 + 10^4.
Thus zero # 10^22 + 1 is actually
1/2 + i * 1,370,919,909,931,995,308,226.68016095...
Values are not guaranteed, and are probably accurate to within 10^(-6) ].
 

3.1     Fractal structure of spacing intervals of adjacent Riemann zeta zeros

           The spacing interval between adjacent zeta zeros for a representative sample of 100 successive zeta zeros starting from the 80,000th value are plotted in Figure 1. The irregular zig-zag pattern of fluctuations of adjacent spacing intervals is identified as characteristic of fractal fluctuations exhibited by dynamical systems ,such as, rainfall, river flows, stock market price index ,etc.(Selvam and Fadnavis, 1998).
 

Figure 1
 

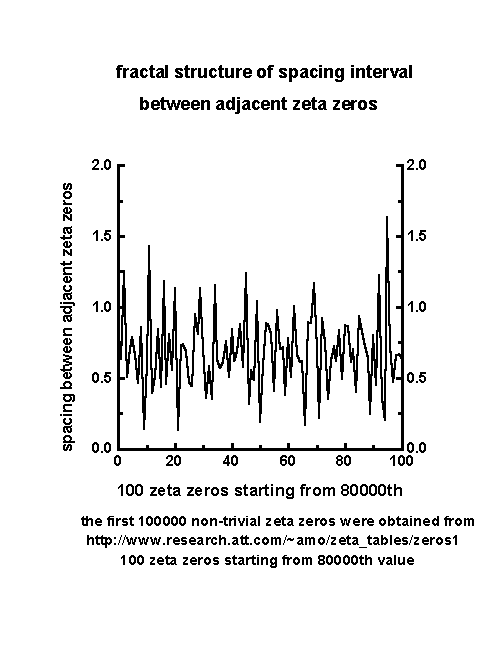
3.2    Continuous periodogram analyses of fractal structure of spacing intervals of adjacent Riemann zeta zeros

    The broadband power spectrum of space-time fluctuations of dynamical systems can be computed accurately by an elementary, but very powerful method of analysis developed by Jenkinson (1977) which provides a quasi-continuous form of the classical periodogram allowing systematic allocation of the total variance and degrees of freedom of the data series to logarithmically spaced elements of the frequency range (0.5, 0). The periodogram is constructed for a fixed set of 10000(m) periodicities Lm which increase geometrically as Lm=2 exp(Cm) where C=.001 and m=0, 1, 2,....m . The data series Yt for the N data points was used. The periodogram estimates the set of Amcos(2pnmS-fm) where Am, nm and fm denote respectively the amplitude, frequency and phase angle for the mth periodicity and S is the time or space interval. In the present study the adjacent spacing intervals for different range of  zeta zeros  were used. The cumulative percentage contribution to total variance was computed starting from the high frequency side of the spectrum. The period T50 at which 50% contribution to total variance occurs is taken as reference and the normalized standard deviation tm values are computed as (Equation 7).

tm = (log Lm / log T50)-1

    The cumulative percentage contribution to total variance, the cumulative percentage normalized phase (normalized with respect to the total phase rotation) and the corresponding t  values were computed. The power spectra were plotted as cumulative percentage contribution to total variance versus the normalized standard deviation t  as given above. The period L is in units of number of class intervals, unit class interval being equal to adjacent spacing interval of zeta zeros in the present study. Periodicities up to T50 contribute up to 50% of total variance. The phase spectra were plotted as cumulative percentage normalized (normalized to total rotation) phase .The variance and phase spectra along with statistical normal distributions are shown in Figures 2 and 3 for two representative data sets of zeta zero spacing intervals. The 'goodness of fit' (statistical chi-square test) between the variance spectrum and statistical normal distribution is significant at <= 5% level. The phase spectrum is close to the statistical normal distribution, but the 'goodness of fit' is not statistically significant. However, the 'goodness of fit' between variance and phase spectra are statistically significant (chi-square test) for individual dominant wavebands (Figures 4 and 5).

Figure 2






 
 

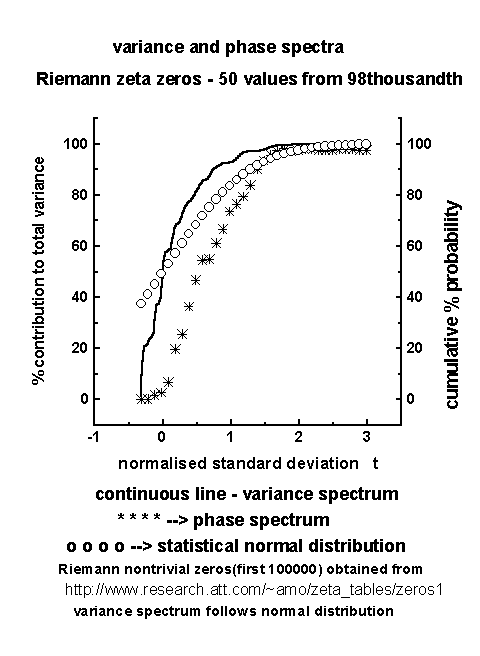
Figure 3







 
 

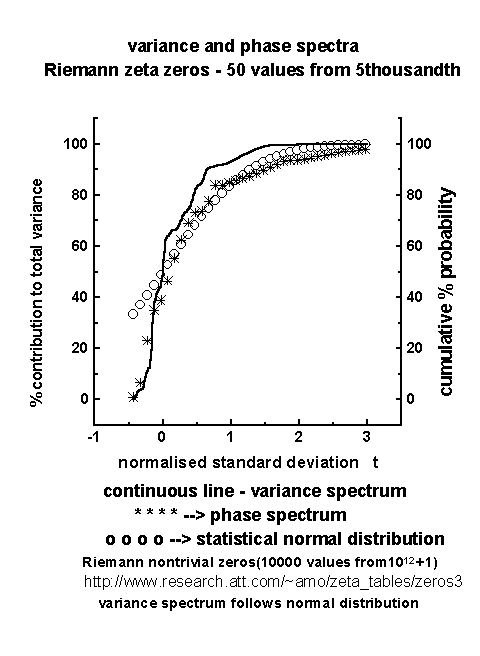
Figure 4









 
 

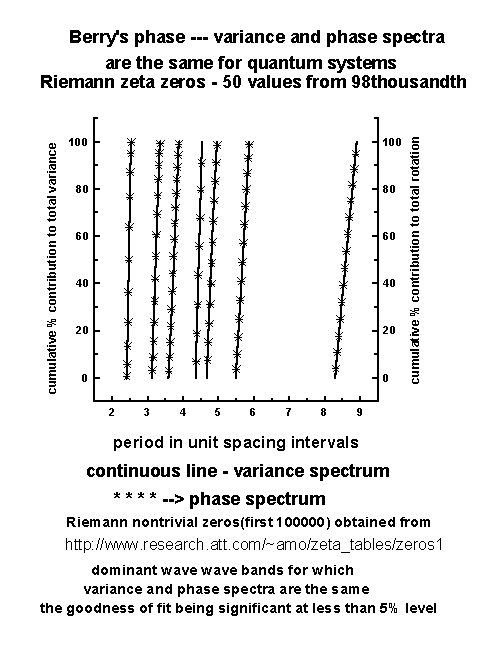
Figure 5







 

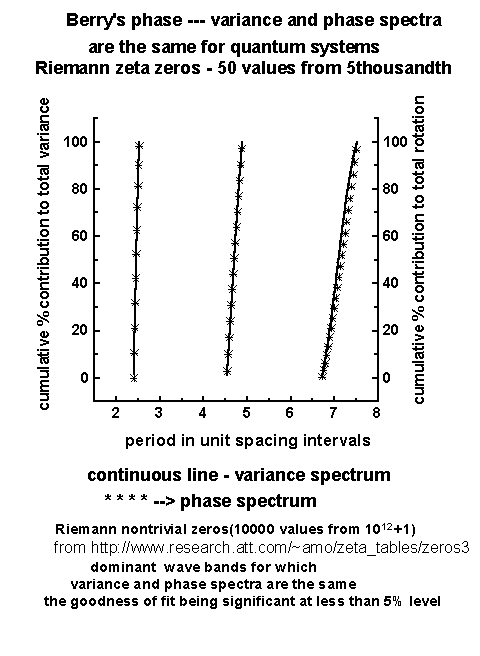
   3.3    Results of power spectral analyses

    Continuous periodogram analyses of the fractal fluctuations of Riemann zeta zeros was done for a large number of data sets and the results are given in Tables1 and 2.
    Table 1 lists the following: (a) details of data files (b) data series location in the data file (c) number of values (d) mean and standard deviation of the data series (e) whether the data series follow statistical normal distribution (f) the value of t50 which is the length scale up to which the cumulative percentage contribution to total variance is equal to 50 (g) whether the variance and phase spectra follow statistical normal distribution characteristics. The length of the data sets ranged from 50 to 10,000 values.
    Results of power spectral analyses of Riemann zeta zero spacing intervals agree with the following model predictions: (a) almost all variance spectra follow statistical normal distribution (b) The magnitude of  t50 values are very close to model predicted value of 3.6 unit spacing intervals( see equation 8 ).

Table 1

Results of power spectral analyses of spacing intervals of adjacent Riemann zeta zeros (non-trivial): comparision with statistical normal distribution


filename
Beginning from
no. of values
mean
standard deviation
t50
power spectra
cvar=cnor
cumphs=cnor
zeros5
1
100
.1354
.0518
2.9658
S
N
zeros5
1
500
.1343*
.0605
3.0016
S
S
zeros5
1
1000
.1342*
.0579
3.0287
S
N
zeros5
1
1500
.1342*
.0583
3.0930
S
N
zeros5
1
2000
.1342*
.0583
3.0076
S
S
zeros5
1
3000
.1342*
.0574
3.0136
S
N
zeros5
1
4000
.1342*
.0566
3.0106
S
N
zeros5
1
5000
.1342*
.0567
3.0016
S
S
zeros5
5000
100
.1354
.0549
2.7931
S
S
zeros5
5000
500
.1343*
.0546
3.0899
S
S
zeros5
5000
1000
.1343*
.0573
2.9926
S
N
zeros5
5000
1500
.1343*
.0565
3.0136
S
S
zeros4
1
100
.1415
.0640
3.0531
S
S
zeros4
1
500
.1410*
.0630
3.1681
S
S
zeros4
1
1000
.1409*
.0604
3.1618
S
N
zeros4
1
1500
.1410*
.0590
3.1335
S
N
zeros4
1
2000
.1410*
.0586
3.1650
S
N
zeros4
1
3000
.1409*
.0595
3.1492
S
N
zeros4
1
4000
.1409*
.0597
3.2032
S
S
zeros4
1
5000
.1410*
.0592
3.2321
S
S
zeros4
5000
100
.1403
.0524
2.8638
S
N
zeros4
5000
500
.1409*
.0590
2.8695
S
N
zeros4
5000
1000
.1408*
.0587
2.8926
S
N
zeros4
5000
1500
.1409*
.0589
2.8753
S
N
zeros3
1
100
.2584
.0938
3.1429
S
S
zeros3
1
500
.2571*
.1053
3.0838
S
S
zeros3
1
1000
.2567*
.1063
3.0076
S
N
zeros3
1
1500
.2568*
.1076
3.0592
S
N
zeros3
1
2000
.2568*
.1071
2.9836
S
N
zeros3
1
3000
.2568*
.1084
3.0899
S
N
zeros3
1
4000
.2568*
.1076
3.0016
S
S
zeros3
1
5000
.2567*
.1079
3.0745
S
N
zeros3
5000
50
.2561
.0956
3.3911
S
S
zeros3
5000
100
.2575
.0926
3.4115
S
S
zeros3
5000
500
.2568*
.1025
3.1335
S
S
zeros3
5000
1000
.2568*
.1061
3.0257
S
N
zeros3
5000
1500
.2568*
.1054
3.0409
S
N
zeros1
1
100
2.2364*
1.0433
3.9636
N
N
zeros1
1
500
1.5973*
.7530
3.9281
N
N
zeros1
1
1000
1.4063*
.6564
3.7740
N
N
zeros1
1
1500
1.3117*
.6075
3.6080
N
S
zeros1
1
2000
1.2512*
.5752
3.6044
N
N
zeros1
1
3000
1.1733*
.5342
3.4909
N
N
zeros1
1
4000
1.1234*
.5082
3.5649
N
N
zeros1
1
5000
1.0870*
.4895
3.4149
N
N
zeros1
5000
100
.9283*
.3640
2.8438
S
N
zeros1
5000
500
.9231*
.3638
2.8753
S
N
zeros1
5000
1000
.9180*
.3630
2.8695
S
N
zeros1
5000
1500
.9134*
.3610
2.8926
S
N
zeros1
5000
10000
.8593*
.3427
2.9777
S
S
zeros1
5000
5000
.8860*
.3512
2.9540
S
N
zeros1
10000
10000
.8169*
.3262
3.0378
S
N
zeros1
80000
10000
.6799*
.2747
3.0961
S
N
zeros1
80000
100
.6869*
.2809
2.9866
S
S
zeros1
98000
50
.6659
.2950
2.7792
S
N
zeros1
98009
50
.6752
.2690
3.1968
S
S
zeros5
1
9999
.1342*
.0563
3.1808
S
N
zeros4
1
9999
.1409*
.0597
3.0167
S
N
zeros3
1
9999
.2567*
.1079
3.0439
S
N

* indicates that the data does not follow statistical normal distribution.
t50 is in terms of unit class interval (equal to the spacing interval between adjacent zeta zeros). Periodicities upto t50 contribute up to 50% to the total variance.
cvar denotes cumulative variance spectrum.
cumphs denotes cumulative phase spectrum.
cnor denotes cumulative normal distribution(statistical).
S denotes statistical significance for 'goodness of fit' at less than or equal to 5% level.
N denotes not statistically significant for 'goodness of fit'.

    Table2 gives the following additional results for the same data sets tabulated in Table 1: (a) The total number of dominant wavebands (b) The percentage number of dominant wavebands with dominant peak periodicities in class intervals 2 - 3, 3 - 4, 4 - 6, 6 - 12, 12 - 20, 20 - 30, 30 - 50, 50 - 80. These wavebands include the model predicted(Equation 2) dominant peak periodicities(or length scales)
 2.2, 3.6, 5.8, 9.5, 15.3, 24.8, 40.1, and 64.9 (in unit spacing intervals of zeta zeros) for values of n ranging from -1 to 6. (c) Also listed are , the actual number of dominant wavebands(nomtot), the number of statistically significant wavebands(nomsg), and wavebands(nombe) which exhibit Berry's phase , namely, the variance spectrum follows closely the phase spectrum (see Section 2).

Table 2

Results of power spectral analyses of spacing intervals of adjacent Riemann zeta zeros (non-trivial): dominant wavebands


file name
begin from
no.of values
no. of dominant wavebands
% no. of dominant wavebands in Class intervals
2-3
3-4
4-6
6-12
12-20
20-30
30-50
50-80
zeros5
1
100
14
nomtot
nomsg
nombe
42.9
6
3
3
21.4
3
0
2
14.3
2
0
2
14.3
2
0
1
7.1
1
0
1
zeros5
1
500
64
nomtot
nomsg
nombe
51.6
33
8
7
18.7
12
4
6
18.7
12
2
5
10.9
7
1
4
zeros5
1
1000
145
nomtot
nomsg
nombe
42.1
61
21
4
22.8
33
5
2
17.9
26
3
9
11.0
16
2
4
4.8
7
0
2
1.4
2
0
2
zeros5
1
1500
214
nomtot
nomsg
nombe
38.8
83
24
0
24.8
53
10
0
18.7
40
8
2
12.1
26
1
2
4.2
9
0
4
0.9
2
0
2
0.5
1
0
1
zeros5
1
2000
264
nomtot
nomsg
nombe
34.5
91
32
0
25.8
68
10
0
19.7
52
6
0
14.4
38
1
1
4.2
11
0
2
0.8
2
0
2
0.4
1
0
1
0.4
1
0
1
zeros5
1
3000
314
nomtot
nomsg
nombe
32.5
102
49
0
22.0
69
26
0
21.3
67
6
0
19.1
60
1
0
3.5
11
0
2
1.0
3
0
2
0.3
1
0
1
0.3
1
0
1
zeros5
1
4000
363
nomtot
nomsg
nombe
28.1
102
60
0
19.8
72
26
0
23.7
86
10
0
23.4
85
1
0
3.3
12
5
2
0.8
3
2
2
0.5
2
0
1
0.3
1
0
1
zeros5
1
5000
393
nomtot
nomsg
nombe
27.2
107
63
0
19.9
78
28
0
21.9
86
14
0
26.2
103
1
0
3.3
13
8
0
0.8
3
2
1
0.5
2
1
1
0.3
1
0
1
zeros5
5000
100
14
nomtot
nomsg
nombe
42.9
6
1
3
7.1
1
0
1
21.4
3
0
1
28.6
4
0
3
zeros5
5000
500
74
nomtot
nomsg
nombe
41.9
31
8
5
17.6
13
2
4
21.6
16
3
7
17.6
13
0
7
1.3
1
0
0
zeros5
5000
1000
161
nomtot
nomsg
nombe
42.9
69
21
1
19.3
31
4
2
19.3
31
4
4
13.0
21
0
5
3.7
6
0
2
1.2
2
0
2
0.6
1
0
1
zeros5
5000
1500
234
nomtot
nomsg
nombe
37.2
87
26
0
20.5
48
7
0
20.5
48
6
1
16.2
38
2
4
3.9
9
0
5
0.9
2
0
2
0.4
1
0
1
0.4
1
0
1
zeros4
1
100
17
nomtot
nomsg
nombe
29.4
5
2
4
29.4
5
1
5
29.4
5
0
4
11.8
2
0
2
zeros4
1
500
82
nomtot
nomsg
nombe
45.1
37
8
5
19.5
16
2
7
24.4
20
1
10
11.0
9
0
4
zeros4
1
1000
175
nomtot
nomsg
nombe
39.4
69
14
0
17.1
30
6
1
21.7
38
3
3
14.9
26
0
6
5.1
9
0
4
1.1
2
0
2
0.6
1
0
0
zeros4
1
1500
230
nomtot
nomsg
nombe
39.6
91
23
0
17.8
41
10
2
22.2
51
4
0
15.2
35
0
2
3.9
9
0
4
0.9
2
0
2
0.4
1
0
1
zeros4
1
2000
275
nomtot
nomsg
nombe
34.2
94
33
0
20.7
57
17
1
21.8
60
6
0
18.5
51
0
0
3.3
9
0
5
0.7
2
0
2
0.4
1
0
1
0.4
1
0
1
zeros4
1
3000
351
nomtot
nomsg
nombe
29.6
104
46
0
18.2
64
19
0
27.1
95
12
0
21.1
74
1
0
2.6
9
2
4
0.9
3
2
2
0.3
1
0
1
0.3
1
0
1
zeros4
1
4000
380
nomtot
nomsg
nombe
27.4
104
48
0
18.2
69
32
0
26.1
99
14
0
24.5
93
2
0
2.4
9
9
1
0.8
3
2
2
0.5
2
1
1
0.3
1
0
1
zeros4
1
5000
385
nomtot
nomsg
nombe
26.7
103
52
0
17.4
67
37
0
23.4
90
19
0
28.3
109
4
0
2.6
10
9
1
0.8
3
2
0
0.5
2
1
1
0.3
1
0
1
zeros4
5000
100
10
nomtot
nomsg
nombe
60.0
6
3
4
20.0
2
0
1
20.0
2
0
0
zeros4
5000
500
77
nomtot
nomsg
nombe
45.5
35
12
7
23.4
18
2
3
14.3
11
0
6
15.6
12
0
6
1.3
1
0
0
zeros4
5000
1000
148
nomtot
nomsg
nombe
39.2
58
14
3
23.7
35
4
4
20.3
30
1
0
11.5
17
0
4
3.4
5
0
2
1.3
2
0
2
0.7
1
0
1
zeros4
5000
1500
215
nomtot
nomsg
nombe
37.7
81
24
0
24.2
52
8
0
20.9
45
2
1
11.2
24
0
2
4.2
9
0
6
0.9
2
0
2
0.5
1
0
1
0.5
1
0
1
zeros3
1
100
16
nomtot
nomsg
nombe
50.0
8
1
5
18.7
3
1
3
18.7
3
1
2
12.5
2
0
2
zeros3
1
500
89
nomtot
nomsg
nombe
44.9
40
9
3
21.3
19
4
7
19.1
17
0
5
10.1
9
0
8
2.3
2
0
2
1.1
1
0
1
1.1
1
0
1
zeros3
1
1000
147
nomtot
nomsg
nombe
41.5
61
17
1
21.8
32
8
3
24.5
36
0
0
8.8
13
4
10
2.0
3
2
3
0.7
1
0
1
0.7
1
0
1
zeros3
1
1500
202
nomtot
nomsg
nombe
43.1
87
24
0
22.8
46
11
1
24.7
50
1
1
6.9
14
9
6
1.5
3
2
3
0.5
1
1
1
0.5
1
0
1
zeros3
1
2000
234
nomtot
nomsg
nombe
42.7
100
32
0
25.2
59
13
1
22.2
52
3
0
7.7
18
13
3
1.3
3
2
2
0.4
1
1
1
0.4
1
1
1
zeros3
1
3000
273
nomtot
nomsg
nombe
40.7
111
45
0
25.3
69
19
0
25.3
69
22
0
7.0
19
14
0
1.1
3
2
1
0.4
1
1
1
0.4
1
1
1
zeros3
1
4000
250
nomtot
nomsg
nombe
38.4
96
51
0
25.2
63
25
0
26.4
66
36
0
7.6
19
15
0
1.6
4
3
1
0.4
1
1
1
0.4
1
1
1
zeros3
1
5000
266
nomtot
nomsg
nombe
38.7
103
61
0
26.7
71
32
0
24.1
64
44
0
7.9
21
15
0
1.9
5
3
0
0.4
1
1
1
0.4
1
1
1
zeros3
5000
50
6
nomtot
nomsg
nombe
33.3
2
1
1
16.7
1
1
0
33.3
2
0
1
16.7
1
0
1 
zeros3
5000
100
21
nomtot
nomsg
nombe
33.3
7
1
4
19.1
4
1
4
23.8
5
0
5
14.3
3
0
2
9.5
2
0
2
zeros3
5000
500
90
nomtot
nomsg
nombe
45.6
41
8
4
17.8
16
2
3
17.8
16
2
8
14.4
13
0
8
2.2
2
0
2
1.1
1
0
1
1.1
1
0
1
zeros3
5000
1000
152
nomtot
nomsg
nombe
43.4
66
20
1
19.7
30
7
3
23.0
35
4
4
10.5
16
2
4
2.0
3
2
2
0.7
1
0
1
0.7
1
0
1
zeros3
5000
1500
190
nomtot
nomsg
nombe
44.2
84
28
1
21.6
41
7
0
21.1
40
6
1
10.5
20
9
4
1.6
3
2
3
0.5
1
1
1
0.5
1
0
1
zeros1
1
100
17
nomtot
nomsg
nombe
47.1
8
0
5
17.7
3
0
3
17.7
3
0
3
0.0
0
0
0
0.0
0
0
0
11.7
2
0
2
0.0
0
0
0
0.0
0
0
0
zeros1
1
500
80
nomtot
nomsg
nombe
45.0
36
4
2
21.3
17
0
3
18.7
15
0
2
8.7
7
0
2
0.0
0
0
0
0.0
0
0
0
5.0
4
0
2
0.0
0
0
0
zeros1
1
1000
150
nomtot
nomsg
nombe
48.0
72
6
0
25.3
38
0
0
14.7
22
0
0
8.0
12
0
0
0.0
0
0
0
0.0
0
0
0
1.3
2
0
2
2.0
3
0
1
zeros1
1
1500
220
nomtot
nomsg
nombe
48.6
107
15
0
22.3
49
1
0
16.8
37
0
0
9.1
20
0
0
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
2.73
6
0
2
zeros1
1
2000
272
nomtot
nomsg
nombe
41.5
113
17
0
23.9
65
0
0
22.8
62
0
0
8.5
23
0
0
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
2.94
8
0
2
zeros1
1
3000
317
nomtot
nomsg
nombe
34.4
109
30
0
27.4
87
7
0
26.2
83
0
0
8.8
28
0
0
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
1.89
6
0
0
zeros1
1
4000
333
nomtot
nomsg
nombe
32.7
109
36
0
26.1
87
7
0
27.6
92
1
0
10.2
34
0
0
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
zeros1
1
5000
330
nomtot
nomsg
nombe
30.6
101
54
0
24.9
82
12
0
27.3
90
3
0
13.6
45
1
0
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
zeros1
5000
100
15
nomtot
nomsg
nombe
60.0
9
3
4
13.3
2
1
1
13.3
2
1
1
13.3
2
1
1
zeros1
5000
500
43
nomtot
nomsg
nombe
67.4
29
8
1
16.3
7
3
0
7.0
3
2
1
9.3
4
2
0
zeros1
5000
1000
62
nomtot
nomsg
nombe
85.5
53
9
0
8.1
5
2
0
3.2
2
2
0
3.2
2
2
0
zeros1
5000
1500
81
nomtot
nomsg
nombe
79.0
64
19
0
16.1
13
2
0
2.5
2
2
0
2.5
2
2
0
zeros1
5000
10000
179
nomtot
nomsg
nombe
55.9
100
77
0
33.5
60
32
0
6.1
11
3
0
1.7
3
3
0
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
zeros1
5000
5000
160
nomtot
nomsg
nombe
64.4
103
61
0
20.6
33
10
1
12.5
20
1
0
1.3
2
2
0
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
zeros1
10000
10000
158
nomtot
nomsg
nombe
58.9
93
65
0
25.9
41
29
0
12.0
19
3
1
1.3
2
2
1
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
0.0
0
0
0
zeros1
80000
10000
98
nomtot
nomsg
nombe
81.6
80
49
0
10.2
10
6
1
5.1
5
4
0
2.0
2
2
0
1.0
1
1
0
zeros1
80000
100
21
nomtot
nomsg
nombe
42.9
9
2
7
28.6
6
0
6
19.1
4
1
4
4.8
1
0
1
4.8
1
0
1
zeros1
98000
50
9
nomtot
nomsg
nombe
33.3
3
2
1
22.2
2
0
2
33.3
3
0
3
11.1
1
0
1
zeros1
98009
50
11
nomtot
nomsg
nombe
45.5
5
1
2
18.2
2
0
0
18.2
2
0
2
9.1
1
0
1
9.1
1
0
1
zeros1
98000
50
9
nomtot
nomsg
nombe
33.3
3
2
1
22.2
2
0
2
33.3
3
0
3
11.1
1
0
1
zeros5
1
9999
410
nomtot
nomsg
nombe
27.6
113
79
0
16.8
69
43
0
22.9
94
36
0
27.6
113
33
0
3.4
14
11
0
1.0
4
2
0
0.5
2
1
0
0.2
1
1
1
zeros4
1
9999
389
nomtot
nomsg
nombe
24.4
95
77
0
17.7
69
42
0
26.0
101
33
0
27.3
106
32
0
2.8
11
9
0
1.0
4
2
0
0.5
2
1
0
0.3
1
1
0
zeros3
1
9999
257
nomtot
nomsg
nombe
38.5
99
81
0
28.4
73
51
0
21.8
56
43
0
7.4
19
17
0
1.6
4
3
0
1.2
3
1
0
1.2
3
1
0

 

unit class interval is equal to the spacing between adjacent zeta zeros(non-trivial).

nomtot  denotes the total number of dominant wavebands in each class interval.

nomsg denotes the number of statistically significant (<= 5%) wavebands in each class interval.

nombe denotes the number of wavebands where the variance and phase spectra are the same, a manifestation of Berry's phase in quantum systems.

4.    Discussions and Conclusions

    The spacing intervals of adjacent Riemann zeta zeros(non-trivial) exhibit fractal fluctuations ubiquitous to dynamical systems in nature. Fractal fluctuations are irregular or chaotic and has emerged (since 1980s) as a subject of intensive study in the new multidisciplinary science of Nonlinear Dynamics and Chaos (Gleick, 1987; Gutzwiller,1990; Jurgen et al ., 1990; Bassingthwaighte and Beyer,1991; Deering and West 1992; Stewart,1998). Power spectra of fractal  fluctuations exhibit inverse power law form indicating long-range space-time correlations identified as self-organized criticality (Bak et al ., 1987;1988; Bak and Chen, 1989,1991; Goldberger et al., 1990; Schroeder, 1991; Stanley, 1995; Ghashghaie et al ., 1996; Buchanan, 1997; Newman, 2000). Also, inverse power law form for power spectra indicate that an eddy continuum underlies the apparently irregular(or chaotic) fractal fluctuations, i.e., the superimposition of an ensemble of eddies( say, such as sine waves) generates the observed fractal fluctuations. A cell dynamical system model developed by the author provides unique quantification for the power spectra of fractal fluctuations in terms of the statistical normal distribution such that the variance represents the probabilities. In summary, fractal fluctuations imply quantum-like chaos in dynamical systems for the following reasons: (a) The superimposition of an ensemble of eddies or waves results in the observed fluctuation pattern. (b) The additive amplitudes of the eddies when squared gives the variance which represents the probability densities. Fractal fluctuations therefore exhibit quantum-like chaos in macroscale dynamical systems.
    Continuous periodogram analyses of Riemann zeta zero spacing intervals show that the power spectra follow the universal and unique inverse power law form of the statistical normal distribution. Riemann zeta zero spacing intervals therefore exhibit quantum-like chaos and is consistent with similar studies by the author which have shown that prime number distribution also exhibits quantum-like chaos ( Selvam and Fadnavis,2000; Selvam, 2000). Riemann had shown that the zeta function represents prime number distribution. Observational and computed values of energy level distributions of excited quantum systems appear to follow closely the Riemann zeta zeros and also prime number distribution(Cipra, 1996). The results are consistent with cell dynamical system model prediction that fractal fluctuations are signatures of quantum-like chaos in dynamical systems of all sizes ranging from the subatomic quantum systems to macroscale fluid flows. The Heisenberg uncertainty principle for quantum systems implies unpredictable fluctuations, i.e., fractal space-time fluctuations (Hey and Walters, 1989) which is a signature of quantum-like chaos.
    Results of all the data sets(ranging in length from 50 to 10000 values) show that starting from the high frequency side, periodicities upto model predicted value of about 3.6 unit spacing intervals contribute upto 50% to the total variance.
     A possible physical explanation for the observed close relationship between the Riemann zeta zeros and energy levels of quantum systems is given in the following:
    The individual fractions 1/2, 1/3, 1/4, 1/5, etc., in the expression for the zeta function (Equation 1 ) may represent (a) the probabilities of occurrence of the primary perturbation in successive growth stages in unit length steps of the large eddy and also the length scale ratio of the enclosed primary eddy to the large eddy .  As shown in Equation 2 , this length scale ratio (r/R) represents the variance or eddy energy. Graphically , in the x - y plane (complex plane) , the above fractions raised to the power of the complex number s(=x+iy) represent fractional probabilities corresponding to the phase angle represented by the location co-ordinates x and y (Argand diagram). Therefore the zeta function represents the energy spectrum of quantum systems at any location (x,y). The zeta zeros on the y-axis at x=1/2, therefore represent the eddy energy minima. A rotation by 90 degrees  of these zeta zero locations will give the energy(maximum) spectrum of the quantum system. An eddy or wave circulation is bi-directional by concept and is associated with bimodal, namely formation and dissipation respectively of phenomenological form for manifestation of energy (Mary Selvam, 1990). Since manifestation of energy in phenomenological form occurs only in one-half cycle, the corresponding energy levels occur at x=1/2.

5.    Acknowledgement

    The author is grateful to Dr.A.S.R.Murty for his keen interest and encouragement during the course of this study.
 

References

Anandan, J., 1992: The geometric phase. Nature  360, 307-313.

Bak, P., Tang, C.,and  Wiesenfeld K., 1987: Self-organized criticality : an explanation of 1/f noise. Phys. Rev. Lett. 59, 381-384.

Bak, P.C., Tang, C., and Wiesenfeld, K., 1988: Self-organized criticality. Phys. Rev. A. 38, 364 - 374.

Bak, P., Chen, K., 1989: The physics of fractals. Physica D 38, 5-12.

Bak, P., Chen, K., 1991: Self-organized criticality. Sci. Am., January, 26-33.

Bassingthwaighte, J. B. and Beyer, R. P.,1991:  Fractal correlations in heterogeneous systems. Physica D 53, 71-84.

Berry, M. V.,1988: The geometric phase. Sci. Amer. Dec., 26-32.

Berry, M., 1992: Quantum physics on the edge of chaos. In The New Scientist's Guide to Chaos, (Ed) Nina Hall, Penguin Books, pp.184 - 195.

Buchanan, M., 1997: One law to rule them all. New Scientist 8 Nov., 30-35.

Burroughs, W. J.,1992: Weather Cycles: Real or Imaginary? Cambridge University Press,Cambridge.

Canavero,F.G., Einaudi, F.,1987: Time and space variability of atmospheric processes. J. Atmos. Sci. 44(12),1589-1604.

Capra, F., 1996: The web of life , HarperCollins Publishers, London, pp.311.

Cipra, B., 1996: Prime formula weds number theory and quantum physics. Science 274, 2014-2015.

Deering, W., and West, B. J., 1992: Fractal physiology. IEEE Engineering in Medicine and Biology June, 40-46.

Devlin, K., 1997: Mathematics: The Science of Patterns. Scientific American Library, New York, pp.215.

Ghashghaie, S., Breymann, Peinke, J., Talkner, P., Dodge, Y., 1996: Turbulent cascades in foreign exchange markets. Nature  381, 767-770.

Ghil, M.,1994: Cryothermodynamics : the chaotic dynamics of paleoclimate. Physica D 77,130-159.

Gleick, J., 1987: Chaos : Making a New Science. Viking , New York.

Goldberger, A. L., Rigney, D. R., West, B. J., 1990: Chaos and fractals in human physiology. Sci. Am. 262(2), 42-49.

Gutzwiller, M. C., 1990: Chaos in classical and quantum systems. Interdisciplinary Applied Mathematics, Volume 1, Springer-Verlag, New York, pp.427.

Hey,T. and Walters, P., 1989: The quantum universe. Cambridge university Press, pp.180.

Hogstrom, U., 1985: Von Karman's constant in atmospheric boundary layer now re-evaluated. J. Atmos. Sci. 42, 263-270.

Jenkinson, A. F.,1977: A Powerful Elementary Method of Spectral Analysis for use with Monthly,Seasonal or Annual Meteorological Time Series. Meteorological Office, London, Branch Memorandum No. 57, pp. 1-23.

Jurgen, H., Peitgen, H-O., Saupe, D.1990: The language of fractals. Sci. Amer. 263, 40-49.

Keating, J., 1990: Physics and the queen of mathematics. Physics World April, 46-50.

Klarreich, E., 2000: Prime time. New Scientist 11 November, 32- 36.

Maddox, J., 1988a: Licence to slang Copenhagen ? Nature 332, 581.

Maddox, J., 1988b: Turning phases into frequencies. Nature 334 , 99.

Maddox, J., 1993: Can quantum theory be understood ? Nature 361, 493.

Mary Selvam, A.,1990: Deterministic chaos, fractals and quantumlike mechanics in atmospheric flows. Can. J. Phys. 68, 831-841. http://xxx.lanl.gov/html/physics/0010046

Newman, M., 2000: The power of design. Nature  405, 412-413.

Rae, A., 1988: Quantum-physics: illusion or reality ? Cambridge University Press, New York, p.129.

Richards, D., 1988: Order and chaos in strong fields. Nature 336, 518-519.

Ruhla, C., 1992: The physics of chance. Oxford University Press, Oxford, U. K.,pp.217.

Schroeder, M., 1991: Fractals, Chaos and Powerlaws. W.H.Freeman and Co., N.Y.

Selvam, A. M., and Fadnavis, S., 1998: Signatures of a universal spectrum for atmospheric interannual variability in some disparate climatic regimes. Meteorology and Atmospheric Physics 66, 87-112.
http://xxx.lanl.gov/abs/chao-dyn/9805028

Selvam, A. M., and Fadnavis, S., 2000: Cantorian fractal patterns, quantum-like chaos and prime numbers in atmospheric flows.(to be submitted for Journal publication).
http://xxx.lanl.gov/abs/chao-dyn/9810011

Selvam, A. M., 2000: Quantum-like chaos in prime number distribution and in turbulent fluid flows. (to be submitted for Journal publication).
http://xxx.lanl.gov/html/physics/0005067

Simon, R., Kimble, H. J., Sudarshan, E.C.G., 1988: Evolving geometric phase and its dynamical interpretation as a frequency shift: an optical experiment. Phys.Rev.Letts. 61(1),19-22.

Stanley, H.E., 1995: Powerlaws and universality. Nature  378, 554.

Stewart, I., 1998: Life's other secret . Allen Lane, The penguin press, pp.273.