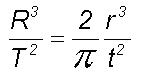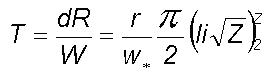The Dynamics of Deterministic Chaos in Numerical
Weather Prediction Models
A. Mary Selvam
Deputy Director (Retired)
Indian Institute of Tropical Meteorology,
Pune 411 008, India
Proc. American Meteorological Society 8th
Conf. Numerical Weather Prediction, February 1988, Baltimore, MD., USA.
1. Introduction
Atmospheric weather systems
are coherent structures consisting of discrete cloud cells forming patterns
of rows/streets, mesoscale clusters (MCC) and spiral bands which maintain
their identity for the duration of their appreciable life times in the
turbulent shear flow of the planetary Atmospheric Boundary Layer (ABL).
The existence of coherent structures (seemingly systematic motion) in turbulent
flows has been well established during the last 20 years of research in
turbulence. It is still, however debated whether these structures are the
consequences of some kind of instabilities (such as shear, or centrifugal
instabilities) or whether they are manifestations of some intrinsic universal
properties of any turbulent flow (Levich, 1987). The coherent cloud structures
in the apparent chaotic (turbulent) flow of the ABL is associated with
large values of Reynold's number (Re) up to 1012 and by convention
is described by the inherently non-linear Navier-Stokes (NS) equations.
Numerical weather prediction models do not give realistic forecasts because
of the following inherent limitations: (1) the non-linear governing equations
for atmospheric flows do not have exact analytic solutions and being sensitive
to initial conditions give chaotic solutions characteristic of deterministic
chaos (2) the governing equations do not incorporate the dynamical interactions
and co-existence of the complete spectrum of turbulent fluctuations which
form an integral part of the large coherent weather systems (Shafee and
Shafee, 1987) (3) limitations of available computer capacity necessitates
severe truncation of the governing equations, thereby generating errors
of approximations (4) the computer precision related roundoff errors magnify
the earlier mentioned uncertainties exponentially with time and the model
predictions become unrealistic (Beck and Roepstorff, 1987). The accurate
modelling of weather phenomena therefore requires alternative concepts
and computational techniques. In this paper a universal theory of deterministic
chaos applicable to the formation of coherent weather structures in the
ABL is presented with the newly identified computational technique "cellular
automata" suitable for computer parallel processing techniques (Hayor,
1987).
2. Deterministic Chaos in
the ABL
The universal period doubling
route to chaos or deterministic chaos is a signature of non-linearity and
is found to occur in disparate physical, chemical and biological systems
(Feigenbaum, 1980; Fairbairn, 1986; Delbourgo, 1986). Feigenbaum established
that the route to chaos is independent of the nonlinear equations describing
the system. Lorenz (1963) showed that deterministic chaos is exhibited
by the three coupled nonlinear ordinary differential equations for a heat
convective system obtained by severe truncation of NS equations. Observational
evidence for the existence of deterministic chaos in the ABL has been established
conclusively by Lovejoy and Schertzer (1986) who showed that the global
cloud cover pattern exhibits fractal geometry which is again a signature
of deterministic chaos. Phenomenological observations of fractal (broken
or fractured) structure in nature represent the two fundamental symmetries
of nature, namely, dilation (r->br) and translation (r->r+c) and correspond
respectively to change in unit of length or in the origin of the co-ordinate
system (Kadanoff, 1986). A selfsimilar object is identified by its fractal
dimension D which is defined as dlnM(R)/dlnR where M(R)
is the mass contained within a distance R from a typical point in
the object. The basic physical mechanism of the observed self-organized
fractal geometry in nature is not yet identified (Kadanoff, 1986).
3. Physics of Deterministic
Chaos in the ABL
The period doubling route
to chaos is basically a growth phenomena whereby large eddy growth is initiated
from the turbulence scale in successive length step increments equal to
the turbulence scale length (Mary Selvam, 1987). In summary, turbulent
eddies of frictional origin at the planetary surface possess an inherent
upward momentum flux which is progressively amplified by buoyant energy
generation from Microscale Fractional Condensation (MFC) of water vapour
on hygroscopic nuclei by deliquescence even in an unsaturated environment
(Pruppacher and Klett, 1978). The exponential decrease of atmospheric density
with height further accelerates the turbulence scale upward momentum flux.
Therefore, the unidirectional (upward) turbulence scale energy pump generates
successively larger vortex roll circulations in the ABL. The larger eddies
carry the turbulent eddies as internal circulations which contribute to
their (large eddies) further growth. Such a process of large eddy growth
is analogous to the emission of anti-Stokes laser emission triggered by
laser pump during chaos in optics (Harrison and Biswas, 1986).
Townsend (1956) has
investigated the structure and dynamics of large eddy formations in turbulent
shear flows and has shown that large eddies of appreciable intensity form
as a chance configuration of the turbulent motion as illustrated in the
following example. Consider a large eddy of radius R which forms
in a field of isotropic turbulence with turbulence length and velocity
scales 2r and w respectively. The mean square circulation
around a circulation path of large eddy radius R is given by
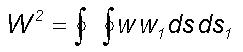where w, w1 are the
tangential velocity components at the positions of the path elements ds
and ds1 . If the velocity product falls to zero while
the separation ds and ds1 is still small compared
with the large eddy radius R , i.e. the motion in sufficiently separated
paths of flow is statistically independent
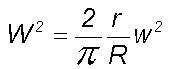
(1)
The above equation can
be applied directly to derive the r.m.s. circulation speed W of
the large eddy of radius R generated by the turbulence scale energy
pump. The scale ratio Z is equal to the ratio of the radii of the
large and turbulent eddies. The environment of the turbulent eddy is a
region of buoyant energy production by condensation (in the troposphere)
and is therefore identified by a Microscale Capping Inversion (MCI) layer
on the large eddy envelope. An incremental growth dR of large eddy
radius equal to the turbulent eddy radius r occurs in association
with an increase dW in large eddy circulation speed as a direct
consequence of the buoyant vertical velocity w* production
per second by MFC. The MCI is thus a region of wind shear and temperature
inversion in the ABL. The growth of large eddies from the turbulence scale
at incremental length steps equal to r - turbulence length scale
doubling - is therefore identified as the universal period doubling route
to chaos in the ABL.
Therefore, considering
turbulence scale yardsticks for length and time, large eddy growth occurs
in discrete unit length steps during unit intervals of time and is analogous
to 'cellular automata' (Hayot, 1987) computational technique where microscopic
domain processes simulate successfully the macroscale flows with simple
no scale (scale invariant) analytic equations. The above concept of deterministic
chaos is also a 'randomly exact' method of determination of macroscale
flow characteristics which is conceived of as a space-time integrated mean
of all inherent non-trivial microscopic domain dynamical processes and
is therefore scale invariant.
The physics of deterministic
chaos therefore enables to identify turbulence as topology dependent and
intrinsic to boundary layer flows, the temperature inversion and wind shear
being manifestations of large eddy growth from turbulent energy generation
processes. This concept is in direct contrast to the conventional view
that inversion layers act as atmospheric lids suppressing convective activity
and that boundary layer turbulence, e.g. Clear Air Turbulence (CAT) is
generated by wind shear in inversion layers, the index of such shear produced
turbulence being measured by the Richardson number (Holton, 1979).
4. Deterministic Chaos and
Atmospheric Eddy Continuum
The turbulent fluctuations
mix overlying environmental air into the growing large eddy volume and
the steady state non-dimensional fractional volume dilution k of
the total large eddy volume across unit cross-section on its envelope is
equal to
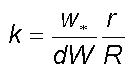
(2)
where w* is the bi-directional
turbulent energy acceleration and dW the corresponding acceleration
of the large eddy circulation during large eddy incremental length step
growth
dR equal to r. From Eq.(1) it may be computed and
shown that
k>0.5 for Z<10. Therefore organized large eddy
growth can occur for scale ratios Z>=10 only since dilution by environmental
mixing is more than half by volume and erases the signature of large eddies
for scale ratios Z<10. Therefore, a hierarchical, scale invariant,
selfsimilar eddy continuum with semi-permanent dominant eddies at successive
decadic scale range intervals is generated by the self-organized period
doubling route to chaos growth process. The large eddy circulation speed
is obtained by integrating Eq.(2) for large eddy growth from the turbulence
scale energy pump at the planetary surface and is given as
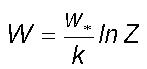
(3)
k=0.4 for Z=10 from Eqs.(1)
and (2). Eq.(3) above is the well known logarithmic wind profile relationship
in the surface ABL and k is designated as the Von Karman's constant
and its value as determined from observations is equal to 0.4 (Hogstrom,
1985). The deterministic chaos model for eddy dynamics in the ABL therefore
predicts that the logarithmic wind profile relationship holds good not
only for the surface friction layer, but throughout the ABL. Also, the
Von Karman's constant, an arbitrary constant of integration in conventional
eddy diffusion theory (Holton, 1979) and determined solely by observations
is now shown to have a physical meaning, namely, a no scale (scale invariant)
quantification of eddy mass exchange and therefore universal for all hydrodynamic
boundary layer fluid flows irrespective of chemical composition and macroscopic
size. Von Karman's constant k is therefore more universal than Feigenbaum's
constants for deterministic chaos. The Feigenbaum's constants for deterministic
chaos are shown in a later section to be functions of k and Z.
4.1 Semi-permanent dominant
eddies (limit cycles) in the ABL
The convective, meso-,
synoptic and planetary scale eddies grow from the turbulence scale by the
eddy mixing process described above (Section 4.0) at successive decadic
scale range intervals. The inherent hierarchy of the atmospheric eddy continuum
is manifested as the Meso-scale Cloud Clusters (MCC) in synoptic scale
weather systems. The relationship between the radius (R), time period
(T), circulation velocity (W) and energy (E) scales
of the convective (c), meso-(m), synoptic(s) and planetary (p) scale atmospheric
systems to the primary turbulence scale (r) is derived from Eq.(1)
and is given below:
(4)
The sun is the main source
of energy which drives the ABL circulations and therefore periodicities
in the weather patterns may finally be related to solar energy input cycles
as shown in the following (1) 40-50 day oscillations in the atmospheric
general circulation and also the ENSO (~5 years) phenomena may result from
the diurnal cycle of solar radiation (1dayx40~40-50 days and 1dayx40x40~
5years) (2) the QBO may result from the semi-diurnal pressure oscillation
(12 hoursx40x40~2 years) (3) the 22 year oscillation in weather patterns
may result from the 5 minute oscillations of the sun's atmosphere (5minsx404
~
22 years).
A continuous periodogram
analysis of high resolution surface pressure values may be used to determine
the amplitude and phase of these semi-permanent atmospheric cycles at different
locations. Eddy energy enhancement at any scale, for e.g. the CO2
related green house warming effect in the convective scale will result
in the total atmospheric eddy continuum energy enhancement (Eq.1) which
may be manifested (1) in the synoptic scale features as intensification
of small scale short duration intense weather systems such as meso-cyclones
and severe local storms. In general seasonal/regional weather anomalies
will intensify as a result of tighter coiling of the circulation patterns
e.g. the prolonged African drought, erratic monsoon activity and abnormal
hurricane tracks. (2) in the planetary scale as an increase in the spatial
and temporal domain of the Hadley -Walker circulations with intensification
of internal structure as mentioned at (1) above. An extension of temperate
rainfall regime to higher latitudes possibly associated with CO2
related global warming has been reported. Further, the ENSO phenomena may
also occur with the shorter period of the QBO. Atmospheric eddy continuum
energy enhancement due to astronomical causes or human activity is therefore
manifested in the first instance as increased variability in global weather
patterns leading to perceptible climate change after an appreciable time
period. The signature of impending weather/climate change, however can
be detected in the geomagnetic H component variations which follow closely
changes in atmospheric circulation patterns as shown in a later section.
5. Deterministic Chaos and
Coherent Helicity
The period doubling route
to chaos growth process therefore generates a scale invariant eddy continuum
where eddy energy flow structure is in the form of nested logarithmic spiral
vortex roll circulations, a complete circulation consisting of the outward
and inherent compensating inward flow. The region of chaos is the dynamic
growth region of large eddy by turbulence scale energy pumping and the
nested vortex hierarchical continuum energy structure is manifested as
the strange attractor design with fractal geometry. The atmospheric circulation
patterns, therefore have fractal dimensions on all scales ranging from
the planetary to the turbulence scale, the strikingly visible pattern of
fractal geometry being exhibited by the clouds. The above concept of the
steady state turbulent atmospheric boundary layer as a hierarchy of intrinsic
helical fluctuations is in agreement with the theoretical investigations
of hydrodynamical turbulence by Levich (1987). All basic meso-scale structures
(less than 1000km in the tropics) appear to be distinctly helical. These
include such outstanding examples of organized geophysical motion as medium
scale tornado generating storms, squall lines, hurricanes, etc. (2) Geophysical
flows give an implicit indication of the upscale transfer of a certain
amount of energy inserted at much smaller scales (3) the helical nature
of the most violent geophysical phenomena - a supercell storm - is shown
beyond any doubt (Lilly, 1986).
The deterministic chaos
model envisages the ABL flow to consist of a web of closed logarithmic
spiral circulations anchored to the earth's surface as a unified whole
single extended object and having visible manifestation in cloud formation
in the troposphere. The atmospheric circulation pattern consisting of dominant
eddies at decadic scale range intervals is analogous to (1) the superstrings
of a 10-dimensional (Z=10) Theory of Everything (TOE) (Fogleman,
1987) (2) the structured quantized vortex roll circulations observed in
superfluid Helium (Mineev et al., 1986) and is also similar to self-sustaining
solitons or solitary waves, in particular, the triple soliton (Tajima,
1987). The fractal geometry to cloud pattern results from the space-time
integration of the non-trivial internal symmetries of the component turbulent
eddies and is therefore a manifestation of supersymmetry in nature.
The fractal dimension
D
of clouds may be expressed as D=dlnP/dlnZ or D=dlnE/dlnZ
where P is the surface pressure, E the eddy kinetic energy
and Z the normalised height. Therefore, the spectral slope of the
eddy energy spectrum will be equal to the fractal dimension D
for the domain Z.
The particles in the
region of chaos follow laws analogous to Kepler's third law of planetary
motion as shown in the following. The periods T and t of
the large and turbulent eddies are respectively given as (2p
R)/W and
(2p
r)/w . Substituting for
W/w
from Eq.(1) gives
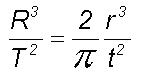R3/T2
is a constant for constant turbulence scale energy pump and therefore large
eddy circulations follow laws analogous to Kepler's third law of planetary
motion. The planetary motions around the sun, the planetary rings around
the major planets and the large atmospheric vortices, e.g. polar vortex
with structured stratospheric Ozone concentration (Kerr, 1986) may all
be manifestations of deterministic chaos.
The rising large eddy
gets progressively diluted by vertical mixing due to turbulent eddy fluctuations
and a fraction f of surface air reaches the normalised height Z
given by
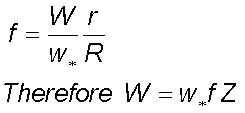From Eqs. (1), (2) and (3)
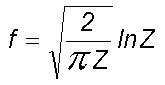The steady state fractional air mass flux
from the surface is dependent only on the dominant turbulent eddy radius.
5.1 Atmospheric eddy dynamics
independent of Coriolis force
Deterministic chaos model
for atmospheric eddy dynamics postulates intrinsic helicity for the solar
insolation related major atmospheric circulations as follows. The major
planetary scale updraft occurs in the local noon time tropical region with
return downdrafts on the local dawn and dusk sectors thereby generating
the semi-diurnal pressure oscillation. The air flow into the noon time
low is from the west and turning anti-clockwise (clockwise) in the northern
(southern) hemispheres because of intrinsic spirality of eddy structures
and not due to Coriolis Force as is assumed generally in conventional meteorological
theory.
6. Deterministic Chaos and
Quantum Mechanics
The kinetic energy KE
per unit mass of an eddy of frequency n
in the hierarchical eddy continuum is shown to be equal to Hnwhere
H
is the spin angular momentum of unit mass of the largest eddy in the hierarchy.
The circulation speed of the largest eddy in the continuum is equal to
the integrated mean of all the inherent turbulent eddy circulations. Let
Wp
be this mean circulation speed or the zero level about which all the larger
frequency fluctuations occur. Therefore
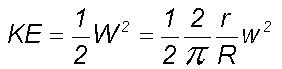from
Eq.(1)
and may be written as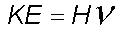 
where
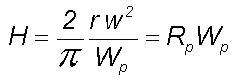H is equal to the product of the momentum
of unit mass of planetary scale eddy and its radius and therefore represents
the spin angular momentum of unit mass of planetary scale eddy about the
eddy center. Therefore the kinetic energy of unit mass of any component
eddy of frequency n
of the scale invariant continuum
is equal to Hn.
Further, since the large eddy is but the sum total of the smaller scales,
the large eddy energy content is equal to the sum of all its individual
component eddy energies and therefore the kinetic energy KE distribution
is normal and the kinetic energy KE of any eddy of radius R
in the eddy continuum expressed as a fraction of the energy content of
the largest eddy in the hierarchy will represent the cumulative normal
probability density distribution. The eddy continuum energy spectrum is
therefore the same as the cumulative normal probability distribution plotted
on a log-log scale and the eddy energy probability density distribution
is equal to the square of the eddy amplitude. Therefore the atmospheric
eddy continuum energy structure follows quantum mechanical laws. The energy
manifestation of radiation and other subatomic phenomena appear to possess
the dual nature of wave and particles since one complete eddy energy circulation
structure is inherently bi-directional and is associated with corresponding
bimodal form of manifested phenomena, e.g. formation of clouds in the updraft
regions and dissipation of clouds in the downdraft regions giving rise
to discrete cellular structure to cloud geometry.
7. Deterministic Chaos and
Statistical Normal Distribution
The statistical distribution
characteristics of natural phenomena follow normal distribution associated
conventionally with random chance. The normal distribution is characterized
by (1) the moment coefficient of skewness equal to zero, signifying symmetry
and (2) the moment coefficient of kurtosis equal to 3 representing
intermittency of turbulence on relative time scale. In the following it
is shown that the universal period doubling route to chaos growth phenomena
in nature gives rise to to the observed statistical normal distribution
parameters as a natural consequence. The period doubling route to growth
is initiated and sustained by the turbulent (fine scale) eddy acceleration
w*
which then propagates by the inherent property of the inertia of the medium.
In the context of atmospheric turbulence, the statistical parameters, mean,
variance, skewness and kurtosis represent respectively the net vertical
velocity, intensity of turbulence, vertical momentum flux and intermittency
of turbulence and are given respectively by w*, w*2,
w*3,
w*4
. By analogy, the perturbation speed w* (motion) per
second of the medium sustained by its inertia represents the mass; w*2
, the acceleration (or force); w*3 , the momentum
(or potential energy) and w*4, the spin angular
momentum, since an eddy motion is inherently symmetric with bidirectional
energy flow, the skewness factor w*3 is equal
to zero for one complete eddy circulation thereby satisfying the law of
conservation of momentum. The momentum coefficient of kurtosis which represents
the intermittency of turbulence is shown in the following to be equal to
3
as a natural consequence of the growth phenomenon by the period doubling
route to chaos. From Eq.(3)
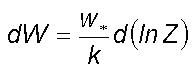
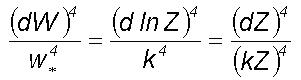
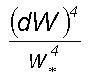represents the statistical moment coefficient of kurtosis. Organized eddy
growth occurs for scale ratio equal to 10 and identifies the large eddy
on whose envelope period doubling growth process occurs. Therefore, for
a dominant eddy
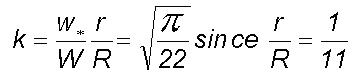(dZ/Z)=1/2 for one length growth by
period doubling process since Z=dZ+dZ. Therefore moment coefficient
of kurtosis is equal to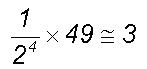 
. In other words, period doubling growth phenomena result in a threefold
increase in the spin angular momentum of the large eddy for each period
doubling sequence. This result is consistent since period doubling at constant
pump frequency involves eddy length step growth dR on either side
of the primary turbulent eddy length dR.
8. The Universal Feigenbaum's
Constants for the ABL
The universal period doubling
route to chaos has been studied extensively by mathematicians, the basic
example with the potential to display the main features of the erratic
behaviour is the Julia model (Delbourgo, 1986) given below.
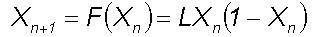The above nonlinear model represents the population
values of the parameter X at different time periods n and
L
parameterises the rate of growth of X for small X. The Eq.(1)
representing large eddy growth as integrated space-time mean of turbulent
eddy fluctuation given as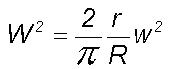 
is
analogous to the Julia model since large eddy growth is dependent on the
energy input from the turbulence scale with ordered two-way energy feedback
between the larger and smaller scales. Feigenbaum's (1980) research showed
that the successive spacing ratios of X and L for adjoining
period doublings are given respectively by the two universal constants
a=-2.5029
and d=4.6692. The universal constants a and d assume
different numerical values for period tripling, quadrupling etc. and the
appropriate values are computed by Delbourgo (1986) and shown to follow
the relation 3d=2a2 over a wide domain.
The physical concept
of large eddy growth by the period doubling process enables to derive the
universal constants a and d and their mutual relationship
as functions inherent to the scale invariant eddy energy structure as follows.
From Eq.(1) the function
a
may be defined as
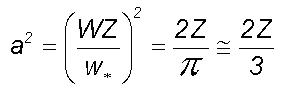
(5)
a is therefore equal to 1/k
from Eq.(2) where k is the Von Karman's constant representing the
non-dimensional steady state fractional volume dilution rate of large eddy
by turbulent eddy fluctuations across unit cross-section on the large eddy
envelope. Therefore 'a' represents the non-dimensional total fractional
mass dispersion rate and is inherently negative and 2a2
represents the bi-directional fractional energy flux into the large eddy
environment. Let d represent the ratio of the spin angular moments
for the total mass of the large and turbulent eddies.
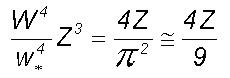
(6)
Therefore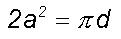 
or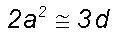 
from
Eqs.(5) and (6). The above equation relating the universal constants is
a statement of the law of conservation of energy, i.e. the period doubling
growth process generates a threefold increase in the spin angular momentum
of the resulting large eddy and propagates outward as the total large eddy
energy flux in the medium. In an earlier section (Section 7) it was shown
that the spin angular momentum of the resulting large eddy accounts for
the observed value of three for the moment coefficient of kurtosis of the
normal distribution. The property of inertia enables propagation of turbulence
scale perturbation in the medium by release of the latent energy potential
of the medium. An illustrative example is the buoyant energy generation
by water vapour condensation in the updraft regions in the ABL.
The universal Feigenbaum's
constants a and d are respectively equal to -2.52
and 4.05 as computed from Eqs.(5) and (6) since the scale ratio
Z
is equal to10 for the self-organized eddy growth mechanism in the
ABL.
9. Deterministic Chaos Model
of Weather Systems
The atmospheric weather
systems are the visible manifestation of the unified atmospheric eddy continuum
in climatologically favourable regions of enhanced buoyant energy generation.
The hierarchical helicity inherent to the turbulent shear flow of the ABL
is manifested as the Mesoscale Cloud Clusters (MCC) in global weather systems,
the cloud bands having inherent curvature (helicity) as exhibited in the
strikingly spiral hurricane cloud bands. The deterministic chaos model
prediction of the universal and unique patterns of cloud bands and
pressure and wind anomaly patterns for synoptic scale weather systems are
compared with well documented observational results for the hurricane system
(Mary Selvam, 1986). The model concepts are given in the following.
Since large eddy growth
involves increase in radius simultaneous with angular displacement from
origin, the trajectory of airflow associated with the large eddies will
follow a logarithmic spiral pattern both in the horizontal and vertical.
The complete eddy circulation consisting of the ascent and the return descent
airflow therefore occurs in the form of logarithmic spiral vortices. The
full continuum of atmospheric eddies exist as a unified whole in the form
of vortices within vortices as displayed in the extreme cases of the tornado
funnel and the dust devil. Large eddy growth is initiated at a single point
location and growth occurs in a spiral wave form analogous to the self-organized
Belousov-Zabotinsky (Ananthakrishnan, 1986) reaction in chemical systems.
In the following, quantitative relations are derived for cloud parameters
as simple analytic equations from considerations of the microscopic scale
dynamics. The angular rotation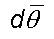 
and
the associated incremental radial growth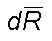 
per
second at any location (R, q )
is given as
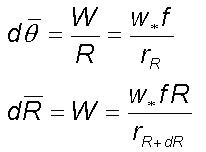
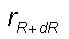denotes
the turbulent eddy radius corresponding to large eddy of radius (R+dR).
The corresponding angle a
between the spiral air flow track of the large eddy and the circle drawn
with radius R is given by
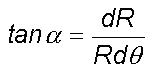substituting b=tan a
and integrating for eddy growth from r to R, the above equation
gives
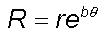This is the equation for an equiangular logarithmic
spiral when the crossing angle a
is a constant. At any location A, the horizontal air flow path into the
eddy continuum system follows a logarithmic spiral track.
9.1 Storm intensity and
cloud band configuration
The cloud bands identify
the circulation path of the synoptic cyclonic eddy whose radial growth
dR
is equal to the dominant turbulent eddy radius and dq
is the corresponding angular rotation.
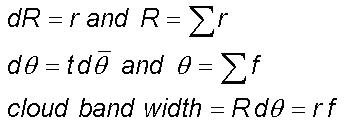The dominant turbulent
eddy radius determines the angular turning dq
and incremental large eddy growth dR and therefore the synoptic
scale spiral cloud band has different crossing angles and band widths at
different locations, with respect to the storm center. Observations show
that increased condensation results in decrease in dominant turbulent eddy
radius. There is heavy condensation close to the storm center in association
with tighter coiling of the spiral with overlapping cloud bands.
9.2 Large eddy growth time
The eddy growth time T
for an eddy of radius R is computed as follows.
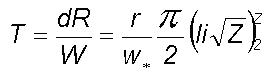where li is the logarithm integral
or Soldner's integral.
9.3 Horizontal profile of
hurricane pressure field
The low pressure field
of the cyclone system is created by the upward ascent of surface air. At
any location distance R from the storm center there is an upward
mass flux of air equal to w*r
per second across unit area where r
is the air density and w* is the buoyant vertical velocity
generated per second by Microscale Fractional Condensation (MFC) at surface
layers. A synoptic scale weather system which has been in existence for
a time period TN and extending to a radial distance RN
develops a central pressure departure equal w*rTN
with respect to the ambient pressure field at the periphery (X). At any
intermediate location (say B) the corresponding pressure departure is equal
to w*rTR
where TR is the time period for the eddy to grow from
B to X. The Normalised Pressure Departure (NPD) at the intermediate location
with respect to the extreme pressure gradient at the storm center is computed
as
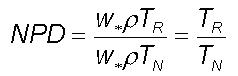
9.4 Horizontal profile of
wind
The horizontal profile
of wind (W) in a cyclone system follows the logarithmic law and
depends only on the turbulent eddy radius from Eq.(3). The airflow speed
is mainly due to the dynamic buoyant energy production by MFC and thus
is not influenced by the rotation of the earth. Therefore the Coriolis
force does not influence the airflow into the synoptic scale eddy
as explained earlier. The universal and unique pressure and wind anomaly
patterns for the hurricane system is in agreement with reported observations
of Holland (1980), Simpson and Riehl (1981) and others.
9.5 Quantum mechanics and
atmospheric weather systems
The quantum reality which
underlies the real world may now be pictured in the context of the universal
theory of chaos as applied to the macroscale cloud/weather systems in the
ABL and may possibly provide physically consistent commonplace solutions
for the apparent inconsistencies and paradoxes (Herbert, 1987) of the quantum
mechanics as follows. The unified atmospheric eddy continuum with its complete
helical vortex roll circulation consists of balanced and instantaneously
adjusting high and low pressure areas of cloud dissipation and formation
respectively and may therefore provide the physical analogue for (1) wave-particle
dulaity (2) non-locality-Berry's phase (3) ultra metric space in sub-atomic
particle dynamics.
9.6 Cloud dynamics, microphysics
and electrification
Cloud growth occurs in
the updraft regions of large eddy circulations under favourable conditions
of moisture supply in the environment. The turbulent eddies inherent to
the large eddies are amplified inside the clouds due to enhanced cloud
water condensation and form "cloud top gravity (buoyancy) oscillations".
The cloud top gravity oscillations are resposible for (1) cloud vertical
mixing and dilution. Downward transport of stratospheric ozone may also
occur in deep convective systems as reported by several workers (2) cloud
electrification by downward transport of naturally occurring negative space
charges from above cloud top regions to the cloud base and simultaneously
the upward transport of positive space charges from lower troposphere to
the cloud top regions thereby generating the observed vertical positive
dipole cloud charge. The Travelling Ionospheric Disturbances (TIDS) have
been attributed to cloud top gravity oscillations in deep convective systems.
The cauliflower-like surface granularity to the cumulus cloud is a signature
of the innumerable turbulent eddies which form the cloud top gravity oscillations.
The deterministic chaos
model enables universal no scale (scale invariant) quantification of the
steady state cloud dynamical, microphysical and electrical processes (Mary
Selvam and Murty, 1985) as listed in the following. (1) The ratio of the
actual cloud liquid water content (q) to the adiabatic liquid water
content (qa) is equal to f, the fraction of surface
air which reaches the normalised height Z after dilution by vertical
mixing due to turbulent eddy fluctuations (2) the vertical profiles of
the vertical velocity W and the total cloud liquid water content
qt
are respectively given by W=w*fZ and qt=q*fZ
where t represents the total values and * represents cloud base
values (3) the cloud growth time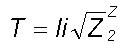 
where
li
is the logarithm integral (4) the cloud dropsize spectrum follows the naturally
occurring Junge aerosol size spectrum and (5) the computed raindrop size
spectrum closely resembles the observed Marshall-Palmer raindrop size distribution
at the surface (6) the electric field at the surface due to the cloud dipole
charge, the strength of the cloud dipole, the cloud electrical conductivity,
the point discharge current are expressed in terms of the basic non-dimensional
parameters f and Z. The above quantitative relations are
universal for all clouds and depends only on the scale ratio Z.
10. Deterministic Chaos,
Atmospheric Electric Field and Geomagnetic Field
Numerous studies indicate
significant correlation between geomagnetic field variations and tropospheric
weather activity (Herman and Goldberg, 1978; Gribbins, 1981; Courtillot
etal.,
1982; Kalinin and Rozanova, 1984; Taylor, 1986). However, the exact physical
mechanism for the observed coupling between meteorological and geomagnetic
phenomena is not yet identified. It may be shown that the atmospheric electric
field and geomagnetic field variations are manifestations of the vertical
mass exchange process between the lower troposphere and ionosphere. The
vertical mass exchange gives rise to upward transport of naturally occurring
positive space charges from surface layers and simultaneous downward transport
of negative space charges from higher levels. The eddy circulations therefore
generate a large scale vertical aerosol current which is of the correct
sign and magnitude to generate the horizontal component of the geomagnetic
field (Mary Selvam, 1987). Therefore atmospheric circulation patterns leave
signature on the geomagnetic field lines whose global variations can be
easily monitored by satellite borne sensors and thus assist in weather
and climate prediction.
Conclusion
The deterministic chaos
model for atmospheric weather systems enables to formulate governing equations
for pressure and wind anomaly patterns in terms of no scale (scale invariant)
quantities by consideration of microscopic scale dynamical processes and
therefore is analogous to 'cellular automata' computational technique.
Parallel processing computers or microprocessors at different locations
can be used to compute real time horizontal and vertical profiles of meteorological
parameters for global weather systems.
References
Anathakrishnan, G., 1986: Self-organization
in physical systems. Bull. Sci. July-August, 20-29.
Beck, C. and G. Roepstorff, 1987: Effects
of phase space discretization on the long time behaviour of dynamical systems.
Physica 25D, 173-180.
Courtillot, V., J. L. Le Mouel, J. Ducruix
and A. Cazenave, 1982: Geomagnetic secular variation as a precursor of
climate change. Nature 297, 386-387.
Delbourgo, R., 1986: Universal facets of chaotic
processes. Asia-Pacific Physics News 1, 7-11.
Fairbairn, W., 1986: Organised chaos: A signature
of nonlinearity. Phys. Bull. 37, 300-302.
Feigenbaum, M. J., 1980: Los Alamos Sci. 1,
4.
Fogleman, G., 1987: Quantum strings. Amer.
J. Phys. 55(4), 330-336.
Gribbins, J. 1981: Geomagnetism and climate.
New Scientist 5 Feb., 350-353.
Harrison, R. G. and D. J. Biswas, 1986: Chaos
in light. Nature 321, 394-401.
Hayot, F., 1987: Viscosity in lattice gas
automata. Physica 26D, 210-214.
Herman, J. R. and R. S. Goldberg, 1978: Sun,
Weather and Climate, NASA SP 426, pp.360.
Hogstorm, U.,1985: Von Karman's constant in
atmospheric boundary layer now reevaluated. J. Atmos. Sci. 42, 263-270.
Kadanoff, L. P., 1986: Fractals: Where's the
physics? Phys. Today Feb. 1986, 6-7.
Levich, E., 1987: Certain problems in the
theory of developed hydrodynamical turbulence. Phys. Rep. Nos. 3, 4, 151,
129-238.
Lilly, D. K., 1986: On the structure, energies
and propagation of rotating convective storms: Part II, Helicity and storm
stabilization. J. Atmos. Sci. 43, 126-140.
Lorenz, E. N., 1963: Deterministic nonperiodic
flow. J. Atmos. Sci. 30, 130-141.
Lovejoy, S. and D. Schertzer, 1986: Scale
invariance, symmetries, fractals and stochastic simulations of atmospheric
phenomena. Bull. Amer. Meteorol. Soc. 67, 21-32.
Mary Selvam, A., 1986: A gravity wave feedback
mechanism for the evolution of the mesoscale cloud clusters (MCC). Proc.
Int'l. Conf. Monsoon and Mesoscale Meteorol., 4-7 Nov., Taipei, Taiwan.
Mary Selvam, A., 1987: Remote sensing of geomagnetic
field and applications to climate prediction. Proc. Int'l Geoscience and
Remote Sensing Symposium (IGARSS '87), 18-21 May, University of Michigan,
USA.
Shaffee, A. and S. Shaffee, 1987: Implication
of the spatial finiteness of mesoscale meteorological fields. Physical
Review A 35, 892-896.
Townsend, A. A., 1956: The structure of turbulent
shear flow. Cambridge University Press, Cambridge, 115-130.