A Superstring Theory for Fractal Spacetime, Chaos and Quantumlike Mechanics in Atmospheric Flows
A. M. Selvam and Suvarna Fadnavis
Indian Institute of Tropical Meteorology, Pune 411 008, India
Website:
http://www.geocities.com/CapeCanaveral/Lab/5833
mailto:suvarna@tropmet.ernet.in
Abstract
Atmospheric flows exhibit long-range spatiotemporal correlations manifested as the fractal geometry to the global cloud cover pattern concomitant with inverse power law form for spectra of temporal fluctuations. Such non-local connections are ubiquitous to dynamical systems in nature and are identified as signatures of self-organized criticality A recently developed cell dynamical system model for atmospheric flows predicts the observed self-organized criticality as a natural consequence of quantumlike mechanics governing flow dynamics. The model is based on the concept that spatial integration of enclosed small scale fluctuations results in the formation of large eddy circulations. The model predicts the following: (a) The flow structure consists of an overall logarithmic spiral trajectory with the quasiperiodic Penrose tiling pattern for the internal structure. (b) Conventional power spectrum analysis will resolve such spiral trajectory as a continuum of eddies with progressive increase in phase (c) Increments in phase are concomitant with increase in period length and also represents the variance, a characteristic of quantum systems identified as 'Berry's phase'. (d) The universal algorithm for self-organized criticality is expressed in terms of the universal Feigenbaum's constants a and d as 2a2=
p d where the fractional volume intermittency of occurrence p d contributes to the total variance 2a2 of fractal structures. (e) The Feigenbaum's constants are expressed as functions of the golden mean. (f) The quantum mechanical constants ' fine structure constant' and 'ratio of proton mass to electron mass' which are pure numbers and obtained by experimental observations only, are now derived in terms of the Feigenbaum's constant a. (g) Atmospheric flow structure follows Kepler's third law of planetary motion. Therefore Newton's inverse square law for gravitation applies to eddy masses also. The centripetal acceleration representing inertial masses (of eddies) are equivalent to gravitational masses. Fractal structure to the space-time continuum can be visualized as a nested continuum of vortex (eddy) circulations whose inertial masses obey Newton's inverse square law of gravitation. The model concepts are equivalent to a superstring model for subatomic dynamics which incorporates gravitational forces.
1. INTRODUCTION
Atmospheric flows exhibit long-range spatiotemporal correlations manifested as the fractal geometry to the global cloud cover pattern concomitant with inverse powerlaw form for power spectra of temporal fluctuations of all scales ranging from turbulence (millimeters-seconds) to climate (thousands of kilometers-years) [1]. Long-range spatiotemporal correlations are ubiquitous to dynamical systems in nature and are identified as signatures of self-organized criticality [2,3]. Standard models for turbulent fluid flows in meteorological theory cannot explain satisfactorily the observed multifractal (space-time) structures in atmospheric flows. Numerical models for simulation and prediction of atmospheric flows are subject to deterministic chaos [4] and give unrealistic solutions. Deterministic chaos is a direct consequence of round-off error growth in iterative computations. Round-off error of finite precision computations doubles on an average at each step of iterative computations [5]. Round-off error will propagate to the mainstream computation and give unrealistic solutions in numerical weather prediction (NWP) and climate models which incorporate thousands of iterative computations in long-term numerical integration schemes. A recently developed non-deterministic cell dynamical system model for atmospheric flows [6-14] predicts the observed self-organized criticality as intrinsic to quantumlike mechanics governing flow dynamics. Further, the fractal space-time structure to the stringlike atmospheric flow trajectory is resolved into a continuum of eddies. The eddy circulations obey Kepler's third law of planetary motion and therefore eddy inertial masses obey Newton's inverse square law of gravitation on all scales from microscopic to macroscale. El Naschie [15-27] has discussed, in a series of publications, the fractal structure to space-time and also states that fractalisation of microspace is the origin of gravity.
2. A NON-DETERMINISTIC CELL DYNAMICAL SYSTEM MODEL FOR FLUID FLOWS: A STRING THEORY FOR FRACTAL SPACETIME
Based on Townsend's [28] concept that large eddies are the envelopes of enclosed turbulent eddy circulations, the relationship between the large and turbulent eddy circulation speeds (W and w
* ) and radii ( R and r ) respectively is given as
![]() (1)
(1)
Since the large eddy is the integrated mean of enclosed turbulent eddy circulations, the eddy energy (kinetic) spectrum follows statistical normal distribution. Therefore, square of the eddy amplitude or the variance represents the probability. Such a result that the additive amplitudes of eddies, when squared, represent the probability densities is obtained for the subatomic dynamics of quantum systems such as the electron or photon [29]. Atmospheric flows, therefore, follow quantumlike mechanical laws. Incidentally, one of the strangest things about physics is that we seem to need two different kinds of mechanics, quantum mechanics for microscopic dynamics of quantum systems and classical mechanics for macroscale phenomena [30-31]. The above visualization of the unified network of atmospheric flows as a quantum system is consistent with Grossing's [32] concept of quantum systems as order out of chaos phenomena. Order and chaos have been reported in strong fields in quantum systems [33].
The square of the eddy amplitude W 2 represents the kinetic energy E given as (from equation .1)
E=Hn (2)
where n (proportional to 1/R ) is the frequency of the large eddy and H is a constant equal to ![]() for growth of large eddies sustained by constant energy input proportional to w* 2 from fixed primary small scale eddy fluctuations. Energy content of eddies is therefore similar to quantum systems which can possess only discrete quanta or packets of energy content hn where h is a universal constant of nature (Planck's constant) and n is the frequency in cycles per second of the electromagnetic radiation. The relative phase angle between large and turbulent eddies is equal to r/R and is directly proportional to W 2 (1). The phase angle therefore represents variance and also there is progressive increase in phase with increase in wavelength. The above relationship between phase angle, variance and frequency has been identified as Berry's Phase [34] in the subatomic dynamics of quantum systems. Berry's phase has been identified in atmospheric flows [14].
for growth of large eddies sustained by constant energy input proportional to w* 2 from fixed primary small scale eddy fluctuations. Energy content of eddies is therefore similar to quantum systems which can possess only discrete quanta or packets of energy content hn where h is a universal constant of nature (Planck's constant) and n is the frequency in cycles per second of the electromagnetic radiation. The relative phase angle between large and turbulent eddies is equal to r/R and is directly proportional to W 2 (1). The phase angle therefore represents variance and also there is progressive increase in phase with increase in wavelength. The above relationship between phase angle, variance and frequency has been identified as Berry's Phase [34] in the subatomic dynamics of quantum systems. Berry's phase has been identified in atmospheric flows [14].
Writing equation (1) in terms of the periodicities T and t of large and small eddies respectively, where
![]()
and
![]()
we obtain
![]() (3)
(3)
Equation (3) is analogous to Kepler's third law of planetary motion, namely, the square of the planet's year (period) to the cube of the planet's mean distance from the Sun is the same for all planets [35]. Newton developed the idea of an inverse square law for gravitation in order to explain Kepler's laws, in particular, the third law. Kepler's laws were formulated on the basis of observational data and therefore are of empirical nature. A basic physical theory for the inverse square law of gravitation applicable to all objects, from macroscale astronomical objects to microscopic scale quantum systems is still lacking. The model concepts are analogous to a string theory [36] where, superposition of different modes of vibration in stringlike energy flow patterns result in material phenomena with intrinsic quantumlike mechanical laws which incorporate inverse square law for inertial forces, the equivalent of gravitational forces, on all scales of eddy fluctuations from macro- to microscopic scales. The cumulative sum of centripetal forces in a hierarchy of vortex circulations may result in the observed inverse square law form for gravitational attraction between inertial masses (of the eddies). Uzer et. al [37] have discussed new developments within the last two decades which have spurred a remarkable revival of interest in the application of classical mechanical laws to quantum systems. The atom was originally visualized as a miniature solar system based on the assumption that the laws of classical mechanics apply equally to electrons and planets. However within a short interval of time the new quantum mechanics of Schrodinger and Heisenberg became established (from the late 1920s) and the analogy between the structure of the atom and that of the solar system seemed invalid and classical mechanics became the domain of the astronomers. There is now a revival of interest in classical and semiclassical methods which are found to be unrivaled in providing an intuitive and computationally tractable approach to the study of atomic, molecular and nuclear dynamics.
The apparent paradox of wave-particle duality in microscopic scale quantum systems [31] is however physically consistent in the context of macroscale atmospheric flows since the bi-directional energy flow structure of a complete atmospheric eddy results in the formation of clouds in updraft regions and dissipation of clouds in downdraft regions. The commonplace occurrence of clouds in a row is a manifestation of wave-particle duality in the macroscale quantum system of atmospheric flows (Fig. 1).
The above-described analogy of quantumlike mechanics for atmospheric flows is similar to the concept of a subquantum level of fluctuations whose space-time organization gives rise to the observed manifestation of subatomic phenomena, i.e. quantum systems as order out of chaos phenomena.
Puthoff [38] has shown that the observed stability of ground-state electronic orbits in atoms is a result of energy exchange with the sea of electromagnetic energy available in the vacuum zero point fluctuations. Historically, quantum mechanics had imposed arbitrary stability criterion for the ground state of electron orbits. Stable ground state is not possible in classical physics since attractive forces between the negative electron and positive nucleus will result in spiraling of orbital electrons into the nucleus accompanied by loss of energy due to emission of radiation by the accelerating electron, since all accelerating charges radiate energy. Puthoff [39] has also put forth the concept of "gravity as a zero-point fluctuation force". The vacuum zero-point fluctuation(electromagnetic) energy is manifested in the Casimir effect [40], namely a force between two closely spaced metal plates. Casimir effect is interpreted as due to imbalances in the zero-point energy caused by the presence of the plates and is analogous to the turbulent scale fluctuations whose spatial integration results in coherent large eddy structures. Recent studies show that background noise enhances weak signals in electronic circuits [41]. El Naschie has proposed in a series of papers [15-27] that Cantorian-fractal conception of spacetime may effect reconciliation between quantum mechanics and gravity.
2.1. Model Predictions
(a) Atmospheric flows trace an overall logarithmic spiral trajectory OR0R1R2R3R4R5 simultaneously in clockwise and anti-clockwise directions with the quasi-periodic Penrose tiling pattern [42] for the internal structure Fig. 2.
The spiral flow structure can be visualized as an eddy continuum generated by successive length step growths OR0 , OR1 , OR2 , OR3 ,....respectively equal to R1 , R2 , R3 ,....which follow Fibonacci mathematical series such that Rn+1 = Rn + Rn-1 and Rn+1 / Rn = t where t is the golden mean equal to (1+Ö 5)/2 ( » 1.618). Considering a normalized length step equal to 1 for the last stage of eddy growth, the successively decreasing radial length steps can be expressed as 1, 1/t , 1/t 2, 1/t 3 ,......The normalized eddy continuum comprises of fluctuation length scales 1, 1/t , 1/t 2, ........ The probability of occurrence is equal to 1/t and 1/t 2 respectively for eddy length scale 1/t in any one or both rotational (clockwise and anti-clockwise) directions. Eddy fluctuation length of amplitude 1/t , has a probability of occurrence equal to 1/t 2 in both rotational directions, i.e. the square of eddy amplitude represents the probability of occurrence in the eddy continuum. Similar result is observed in the subatomic dynamics of quantum systems which are visualized to consist of the superimposition of eddy fluctuations in wave trains (eddy continuum).
Nonlocal connections are intrinsic to quasiperiodic Penrose titling pattern. The phenomenon known as nonlocality or "action at a distance" characterize quantum systems. Experiments in quantum optics show that two distant events can influence each other instantaneously. Nonlocal connections in quantum systems apparently violate the fundamental theoretical law in modern physics that signal transmission cannot exceed the speed of light. The distinction between locality and nonlocality is related to the concept of a trajectory [43] of a single point object. The instantaneous nonlocal connection in the stringlike energy flow patterns which represent extended objects can be visualised as shown in Fig. 3
The circulation flow pattern with center O and radius OU (or OD )represents an eddy. In the medium of propagation, namely, atmosphere (air ) in this case, upward motion U represents convection and cloud formation in association simultaneously with cloud dissipation in downward motion D. There is an instantaneous nonlocal connection between the phases of the particles at U and D . The same concept can be applied to an extended object (Fig. 1 ) such as a row of clouds represented by the wave function y which is the superimposition of a continuum of eddies.
In summary, energy pumping at a fundamental frequency generates a broad-band eddy continuum and has been observed as chaos in laser and non-linear optical systems which are basically governed by quantum mechanical laws [44].
(b) Conventional continuous periodogram power spectral analyses of such spiral trajectories will reveal a continuum of periodicities with progressive increase in phase.
(c) The broadband power spectrum will have embedded dominant wave-bands the bandwidth increasing with period length. The peak periods En in the dominant wavebands will be given by the relation
En = TS(2+t )t n (4)
where t is the golden mean equal to (1+Ö 5)/2 [@ 1.618] and Ts is the primary perturbation time period, for example, the solar powered annual cycle (summer to winter) of solar heating in a study of interannual climate variability. Ghil [45] reports that the most striking feature in climate variability on all time scales is the presence of sharp peaks superimposed on a continuous background. The model predicted periodicities are 2.2, 3.6, 5.8, 9.5, 15.3, 24.8, 40.1 and 64.9 years for values of n ranging from -1 to 6. Periodicities close to model predicted have been reported [46].
(d) The overall logarithmic spiral flow structure is given by the relation
![]() (5)
(5)
where the constant k is the steady state fractional volume dilution of large eddy by inherent turbulent eddy fluctuations . The constant k is equal to 1/t 2 (@ 0.382) and is identified as the universal constant for deterministic chaos in fluid flows. The steady state emergence of fractal structures is therefore equal to
1/k @ 2.62 (6)
The model predicted logarithmic wind profile relationship such as equation (5) is a long-established(observational) feature of atmospheric flows in the boundary layer, the constant k, called the Von Karman 's constant has the value equal to 0.38 as determined from observations. Historically, equation (5), basically an empirical law known as the universal logarithmic law of the wall , first proposed in the early 1930s by pioneering aerodynamicists Theodor von Karman and Ludwig Prandtl, describes shear forces exerted by turbulent flows at boundaries such as wings or fan blades or the interior wall of a pipe. The law of the wall has been used for decades by engineers in the design of aircraft, pipelines and other structures [47].
In equation (5), W represents the standard deviation of eddy fluctuations, since W is computed as the instantaneous r.m.s.(root mean square) eddy perturbation amplitude with reference to the earlier step of eddy growth. For two successive stages of eddy growth starting from primary perturbation w* , the ratio of the standard deviations Wn+1 and Wn is given from equation (5) as (n+1)/n. Denoting by s the standard deviation of eddy fluctuations at the reference level (n=1) the standard deviations of eddy fluctuations for successive stages of eddy growth are given as integer multiples of s , i.e., s , 2s , 3s , etc. and correspond respectively to
statistical normalized standard deviation t = 0,1,2,3, etc. (7)
The conventional power spectrum plotted as the variance versus the frequency in log-log scale will now represent the eddy probability density on logarithmic scale versus the standard deviation of the eddy fluctuations on linear scale since the logarithm of the eddy wavelength represents the standard deviation, i.e. the r.m.s. value of eddy fluctuations (5). The r.m.s. value of eddy fluctuations can be represented in terms of statistical normal distribution as follows. A normalized standard deviation t=0 corresponds to cumulative percentage probability density equal to 50 for the mean value of the distribution. Since the logarithm of the wavelength represents the r.m.s. value of eddy fluctuations the normalized standard deviation t is defined for the eddy energy as
![]()
![]()
![]()
![]() (8)
(8)
where L is the period in years and T50 is the period up to which the cumulative percentage contribution to total variance is equal to 50 and t = 0. LogT50 also represents the mean value for the r.m.s. eddy fluctuations and is consistent with the concept of the mean level represented by r.m.s. eddy fluctuations. Spectra of time series of meteorological parameters when plotted as cumulative percentage contribution to total variance versus t have been shown to follow the model predicted universal spectrum [6-14].
(e) Mary Selvam [5] has shown that equation (1) represents the universal algorithm for deterministic chaos in dynamical systems and is expressed in terms of the universal Feigenbaum's [48] constants a and d as follows. The successive length step growths generating the eddy continuum OR0R1R2R3R4R5 analogous to the period doubling route to chaos (growth) is initiated and sustained by the turbulent (fine scale) eddy acceleration w* which then propagates by the inherent property of inertia of the medium of propagation. Therefore, the statistical parameters mean , variance , skewness and kurtosis of the perturbation field in the medium of propagation are given by w* , w* 2 ,w* 3 ,and w* 4 respectively. The associated dynamics of the perturbation field can be described by the following parameters. The perturbation speed w* (motion) per second (unit time) sustained by its inertia represents the mass, w* 2 the acceleration or force, w* 3 the angular momentum or potential energy, and w* 4 the spin angular momentum, since an eddy motion has an inherent curvature to its trajectory.
It is shown that Feigenbaum's constant a is equal to [5]
![]() (9)
(9)
Where the subscripts 1 and 2 refer to two successive stages of eddy growth. Feigenbaum's constant a as defined above represents the steady state emergence of fractional Euclidean structures. Considering dynamical eddy growth processes, Feigenbaum's constant a also represents the steady state fractional outward mass dispersion rate and a2 represents the energy flux into the environment generated by the persistent primary perturbation w* . Considering both clockwise and counterclockwise rotations, the total energy flux into the environment is equal to 2a2 . In statistical terminology, 2a2 represents the variance of fractal structures for both clockwise and counterclockwise rotation directions.
The Feigenbaum's constant d is shown to be equal to [5]
![]() (10)
(10)
and represents the fractional volume intermittency of occurrence of fractal structures for each length step growth. Feigenbaum's constant d also represents the relative spin angular momentum of the growing large eddy structures as explained earlier.
Equation (1). may now be written as
![]() (11)
(11)
Where dR equal to r represents the incremental growth in radius for each length step growth, i.e. r relates to the earlier stage of eddy growth.
Substituting the Feigenbaum's constants a and d defined above (9 and 10) equation (11) can be written as
2a2 = p d (12)
where p d ,the relative volume intermittency of occurrence contributes to the total variance 2a2 of fractal structures.
In terms of eddy dynamics, the above equation states that during each length step growth, the energy flux into the environment equal to 2a2 contributes to generate relative spin angular momentum equal to p d of the growing fractal structures.
It was shown at equation (6) above that the steady state emergence of fractal structures in fluid flows is equal to 1/k ( = t 2 ) and therefore the Feigenbaum's constant a is equal to
a = t 2 = 1/k = 2.62 (13)
(f) The relationship between Feigenbaum's constant a and statistical normal distribution for power spectra is derived in the following.
The steady state emergence of fractal structures is equal to the Feigenbaum's constant a (6). The relative variance of fractal structure for each length step growth is then equal to a2. The normalized variance 1/a2n will now represent the statistical normal probability density for the nth step growth according to model predicted quantumlike mechanics for fluid flows . Model predicted probability density values P are computed as
P = t - 4 n (14)
or
P = t - 4 t (15)
where t is the normalized standard deviation (7) and are in agreement with statistical normal distribution as shown in Table 1.
The statistical normal distribution characteristics underlie the fractal space-time continuum fluctuations as shown in the following
The steady state emergence of fractal structures for each length step growth for any one direction of rotation ( either clockwise or anticlockwise ) is equal to
![]()
since the corresponding value for both direction is equal to a (6 ).
The emerging fractal space-time structures have moment coefficient of kurtosis given by the fourth moment equal to

The moment coefficient of skewness for the fractal space-time structures is equal to zero for the symmetric eddy circulations. Moment coefficient of kurtosis equal to 3 and moment coefficient of skewness equal to zero characterise the statistical normal distribution underlying the fractal space-time eddy continuum structure.
Normal distribution characteristics for the eddy continuum fluctuation field can also be derived from model concept as follows.
Let P represent the probability of occurrence in the medium of bidirectional eddy energy flux with characteristics of a particular large eddy of radius R. Since W originates from w*
![]()
substituting from equation (1)
![]()
substituting from equation (5)
![]()
Substituting for k , namely,
![]()
![]()
The probability P is obtained as
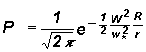
![]() (16)
(16)
For any two successive stages of eddy growth (1)
![]()
therefore
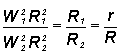
Linearising equation (16) for two successive stages of eddy growth
![]()

![]()
Therefore statistical normal distribution characteristics are followed by the probability P of occurrence of eddy fluctuation W originating from earlier stage perturbation w*.
(g) The power spectra of fluctuations in fluid flows can now be quantified in terms of universal Feigenbaum's constant a as follows.
The normalized variance and therefore the statistical normal distribution is represented by (from equation 14)
P = a - 2t (17)
where P is the probability density corresponding to normalized standard deviation t. The graph of P versus t will represent the power spectrum. The slope S of the power spectrum is equal to
![]() (18)
(18)
The power spectrum therefore follows inverse power law form, the slope decreasing with increase in t. Increase in t corresponds to large eddies ( low frequencies) and is consistent with observed decrease in slope at low frequencies in dynamical systems.
(h) The fractal dimension D can be expressed as a function of the universal Feigenbaum's constant a as follows.
The steady state emergence of fractal structures is equal to a for each length step growth (7 & 13) and therefore the fractal structure domain is equal to am at mth growth step starting from unit perturbation. Starting from unit perturbation, the fractal object occupies spatial (two dimensional) domain am associated with radial extent t m since successive radii follow Fibonacci number series. The fractal dimension D is defined as
![]()
where M is the mass contained within a distance R from a point in the fractal object. Considering growth from nth to (n+m)th step
![]() (19)
(19)
similarly
![]() (20)
(20)
Therefore the fractal dimension D is given as
![]() (21)
(21)
The fractal dimension increases with the number of growth steps. The dominant wavebands increase in length with successive growth steps. The fractal dimension D indicates the number of periodicities which superimpose to give the observed four dimensional space-time structure to the flow pattern. The above concept of dimension for real world spacetime patterns is consistent with El Naschie's[25,26] interpretation of dimensions for superstring theories in particle physics, namely a string rotates in ordinary space and only uses the extra dimensions for vibrations which simulate particle masses. El Naschie has also derived mathematically and shown that the golden mean is intrinsic to the geometry of fractal structures [49-54]. The correlated fluctuations of the fractal spacetime eddy continuum is analogous to the Bose-Einstein condensation phenomena observed in liquid helium [55-58].
(i) The relationship between fine structure constant, i.e. the eddy energy ratio between successive dominant eddies and Feigenbaum's constant a is derived as follows.
2a2 = relative variance of fractal structure (both clockwise and anticlockwise rotation) for each growth step.
For one dominant large eddy (Fig. 2) OR0R1R2R3R4R5 comprising of five growth steps each for clockwise and counterclockwise rotation, the total variance is equal to
2a2 x 10 = 137.07 (22)
For each complete cycle ( comprising of five growth steps each ) in simultaneous clockwise and counterclockwise rotations, the relative energy increase is equal to 137.07 and represents the fine structure constant for eddy energy structure.
Incidentally,the fine structure constant in atomic physics [59-63], designated as a -1 ,a dimensionless number equal to 137.03604, is very close to that derived above for atmospheric eddy energy structure. This fundamental constant has attracted much attention and it is felt that quantum mechanics cannot be interpreted properly until such time as we can derive this physical constant from a more basic theory.
(j) The ratio of proton mass M to electron mass me , i.e. M/me is another fundamental dimensionless number which also awaits derivation from a physically consistent theory. M/me determined by observation is equal to about 2000. In the following it is shown that ratio of energy content of large to small eddies for specific length scale ratios is equivalent to M/me.
From Equation (22),
The energy ratio for two successive dominant eddy growth = (2a2 x10)2
Since each large eddy consists of five growth steps each for clockwise and anticlockwise rotation,
The relative energy content of large eddy with respect to primary circulation structure inside this large eddy
= (2a2 x 10)2/10
@
1879
The primary circulation corresponds to OR0R1 (Fig.2) with length scale OR0 equal to
t 5 and the dominant large eddy length scale OR5 is then equal to (t 5)6 . The length scale ratio OR5 / OR0 is equal to ( t 5 )6 /t 5 = t 25 @ 105.22 . The ratio of the radii of atom and electron is also approximately equal to 105 [64].Quantum mechanical concepts relating to fundamental particles and universal constants are summarised in the following [62]. The only objects that appear to be exactly the same every where are the atoms and their constituent particles. A natural unit of mass is the nucleon mass, equal approximately to that of the hydrogen atom. Nucleons(I. e. , protons and neutrons) have a mass 1836 times the mass of the electron.
The constants of nature can be arranged to form natural numbers (often referred to as dimensionless numbers) that are independent of our units of measurement. The ratio of the nucleon and electron masses equal to approximately 1836 is one such number. Another example is the Sommerfeld's fine structure constant defined by
a
![]()
Where e is the charge on electron, h, the Plank's constant and c, the velocity of light . The fine structure constant appears whenever radiation interacts with particles, and the combination of c, h and e indicates a wave like (h) interaction between particles (e) and light (c)
The classical electron radius is the size of an electron as calculated prior to the introduction of quantum mechanics. It is obtained by assuming that all the energy mec2 of the electron is in the form of electrical energy equal to
![]()
Thus giving a radius r expressed by

A characteristic size of atoms is the radius R of the hydrogen atom
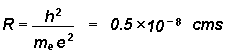
known as the Bohr orbit radius. The absence of the gravitational constant G and c indicates that gravity and relativity are not of primary importance in the structure of atoms.
The electron radius
![]()
Where R is the radius of the hydrogen atom. Therefore ratio of radii of atom to electron is equal to
a -2 » 105Summarising [64]
radius of electron
» 2.82´ 10-13 cms = rradii of most atoms
» 2´ 10-8 cms = RThe scale ratio Z =R/r
» 105The radius of the electron is about one hundred-thousandths of the radius of an average atom [64]
The cell dynamical system model concepts therefore enable physically consistent derivation of fundamental constants which define the basic structure of quantum systems. These two fundamental constants could not be derived so far from a basic theory in traditional quantum mechanics for subatomic dynamics [63].
3. NO SCALE MODEL FOR SUPER GRAVITY
A no scale energy M can be defined for the large eddy energy with respect to the primary eddy energy mp [60-61] as follows
Since phenomenological manifestation of energy occurs only during one half cycle of eddy perturbation
![]() and
and
![]()
from equation (1)
![]()
The above concept is analogous to the no scale super gravity model of Lahanas and Nanapoulous [65] where M, the super-Planck mass is given in terms of the Planck scale mp (
» 1019 Gev ) which corresponds to the first excited state of these strings[66]. The virtues of the no scale super gravity model are automatically vanishing cosmological constant (at least at the classical level), dynamical determination of all mass scales in terms of fundamental Planck scale mp and acceptable low energy phenomenology. The no scale structure is super symmetric since it fuses together the non-trivial internal symmetries of the internal small scale eddies with the spacetime (Poincare) symmetries of the eddy continuum structure and accounts for the observed fractal geometry in nature.The string theory visualises particles as extended objects and thereby avoids singularities, a major problem in the application of point-like concept for particles in traditional physics[67].
The string theory for quantumlike mechanics in atmospheric flows is analogues to Bohm's concept of implicate order for subatomic dynamics of quantum systems [68] .
4. CONCLUSION
The cell dynamical system model presented in the paper is basically a string theory applicable to all dynamical systems ranging from macroscale atmospheric flows to subatomic scale quantum systems. The four dimensional real world spacetime continuum fluctuation are manifestation of the superimposition of a hierarchical continuum of eddy circulations, whose centripetal acceleration add cumulatively to represent the inertial mass, which is equivalent to gravitational mass.
Acknowledgements
The authors express their gratitude to Dr. A. S. R. Murty for his keen interest and encouragement during the course of this study.
REFERENCES
1. Y. Tessier S. Lovejoy P. Hubert D. Schertzer and S. Pecknold. Multifractal analysis and modeling of rainfall and river flows and scaling, casual transfer functions, J. Geophys. Res. 101(D21), 26427-26440 (1996).
2. P. C. Bak C. Tang and K. Wiesenfeld. Self-organized criticality, Phys. Rev. A 38, 364-374 (1988).
3. M. Buchanan. One law to rule them all, New Scientist 8 Nov.,30-35(1997).
4. J. Gleick. Chaos : Making a New Science, Viking , New York (1987).
5. A. Mary Selvam. Universal quantification for deterministic chaos in dynamical systems, Applied Math. Modelling 17, 642-649 (1993)
6. A. M Selvam. The dynamics of deterministic chaos in single mode optical fibre laser transmission, Proc. Nat'l Aerospace and Electronic conference, Naecon, Dayton, Ohio, May 18-22, 200-207 (1987).
7. A. M. Selvam. The dynamics of non-linear effects in optical processes, J. Luminescence 40 & 41, 535-536 (1988).
8. A. Mary Selvam. Deterministic chaos, fractals and quantumlike mechanics in atmospheric flows, Can. J. Phys. 68, 831-841 (1990).
9. A. Mary Selvam J. S. Pethkar and M. K. Kulkarni. Some unique characteristics of atmospheric interannual variability in rainfall time series over India and the United Kingdom, Adv. Atmos. Sci. 12(3), 377-385 (1995).
10. A. Mary Selvam and M. Radhamani. Universal spectrum for short period (days) variability in atmospheric total ozone, Mausam 46(3), 297-302 (1995).
11. A. Mary Selvam and R. R. Joshi. Universal spectrum for interannual variability in COADS global air and sea surface temperatures, Int'l. J. Climatol. 15, 613-624 (1995).
12. . A. Mary Selvam J. S. Pethkar M. K. Kulkarni and R. Vijayakumar. Signatures of a universal spectrum for atmospheric interannual variability in COADS surface pressure time series, Int'l. J. Climatol. 16, 1 -11 (1996).
13. A. Mary Selvam. Quasicrystalline pattern formation in fluid substrates and phyllotaxis, In: D. Barabe and R. V. Jean (eds.), Symmetry in Plants. World Scientific Series No 4. in Mathematical Biology and Medicine, World Scientific, Singapore. (1999).
14. A. Mary Selvam and Suvarna Fadnavis. Signatures of a universal spectrum for atmospheric interannual variability in some disparate climatic regimes, Meteorology and Atmospheric Physics 66, 87-112 (1998 )
15. M. S. El Naschie. Multidimensional Cantor sets in classical and quantum mechanics, Chaos, Solitons and Fractals 2(2), 211-220 (1992).
16. M.S. El Naschie. Statistical mechanics of multidimensional Cantor sets, Godel theorem and quantum spacetime, J. Franklin Institute 330(1), 199-211 (1993).
17. M. S. El Naschie. On certain infinite dimensional Cantor sets and Schrodinger wave, Chaos, Solitons and Fractals 3(1), 89-98 (1993).
18. M. S. El Naschie. Dimensions and Cantor spectra, Chaos, Solitons and Fractals 4(1), 2121-2132 (1994).
19. M. S. El Naschie. Iterated function systems, information and the two-slit experiment of quantum mechanics , Chaos, Solitons and Fractals 4(7), 1141-1145 (1994).
20. M. S. El Naschie. On the nature of complex time and the two-slit experiment, Chaos, Solitons and Fractals 5(6),1031-1032 (1995).
21. M. S. El Naschie. Time symmetry breaking, duality and Cantorion spacetime , Chaos, Solitons and Fractals 7(4), 499-518 (1996).
22. M. S. El Naschie. A note on quantum gravity and Cantorian spacetime, Chaos, Solitons and Fractals 8(1), 131-133 (1997).
23. J. Argyris and C. Ciubotariu. On El Naschie's complex time and gravitation, Chaos, Solitons and Fractals 8(5), 743-751 (1997).
24. M. S. El Naschie. Banach-Tarski theorem and Cantorian micro space-time, Chaos, Solitons and Fractals 8(5), 1503-1508
25. M. S. El.Naschie. Fractal gravity and symmetry breaking in a hierarchical cantorian space, Chaos, Solitons and Fractals 8(11), 1865-1872 (1997).
26 M. S. El Naschie. Remarks on superstrings, fractal gravity, Nagasawa's diffusion and Cantorian space-time, Chaos, Solitons and Fractals 8(11), 1873-1886 (1997).
27. M. S. El Naschie. The Bethe lattice and the dimension of micro spacetime , Chaos, Solitons and Fractals 8(11), 1887-1889 (1997).
28. A. A. Townsend. The Structure of Turbulent Shear Flow. Cambridge University Press, London, U.K. (1956).
29. J. Maddox . Licence to slang Copenhagen ? Nature 332, 581 (1988).
30. J. Maddox. Can quantum theory be understood ? Nature 361, 493 (1993).
31. A. Rae. Quantum-Physics: lllusion or Reality ? Cambridge University Press, New York (1988).
32. G. Grossing. Quantum systems as order out of chaos phenomena, Il Nuovo Cimento, 103B , 497-510 (1989).
33. J. Brown. Where two worlds meet, New Scientist,18 May, 26-30 (1996).
34. M. V. Berry. The geometric phase, Sci. Amer. Dec., 26-32 (1988).
35. S. Weinberg,. Dreams of a Final Theory. Vintage, (1993).
36. M. Kaku. Into the eleventh dimension, New Scientist 18 Jan, 32-36 (1997).
37. T. Uzer D. Farrelly J. A. Milligan P. E. Raines and J. P. Skelton . Celestial mechanics on a microscopic scale, Science. 253, 42-48 (1991).
38. H. E. Puthoff. Ground state of hydrogen as a zero-point fluctuation-determined state, Phys. Rev. D 35, 3266 (1987).
39. H. E. Puthoff. Gravity as a zero-point fluctuation force, Phys. Rev A 39, 2333 (1989).
40. L. Spruch. Long-range (Casimir) interactions, Science 272,1452-1455(1996).
41. F. Moss and K. Wiesenfeld. The Benefits of background noise, Sci. Am. Aug., 50-53 (1995).
42.. P. Steinhardt. 1997: Crazy crystals, New Scientist 25 Jan, 32-35 (1997).
43. R. Y. Chiao P. G. Kwiat and A. M. Steinberg. Faster than light, Sci. Am. Aug., 38-46 (1993).
44. R. G. Harrison and D. G. Biswas. Chaos in light, Nature
321, 394-401 (1985).45. M. Ghil. Cryothermodynamics : The chaotic dynamics of paleoclimate, Physica D 77,130-159 (1994).
46. W. J. Burroughs. Weather Cycles: Real or Imaginary?. Cambridge University Press, Cambridge (1992).
47 B. Cipra. A new theory of turbulence causes a stir among experts. Science 272, 951 (1996).
48. M. J. Feigenbaum. Universal behavior in nonlinear systems, Los Alamos Sci., 1, 4-27 (1980).
49. M. S. El Naschie. Complex dynamics in a 4D Peano-Hilbert space, Il Nuovo Cimento 107B(5), 583-594(1992).
50. M. S. El Naschie. Penrose tiling, semi-conduction and Cantorian 1/fa spectra in four and five dimensions, Chaos, Solitons and Fractals 3(4), 489-491 (1993).
51. M. S. El Naschie. On dimensions of Cantor set related systems, Chaos, Solitons and Fractals 3(6), 675-685 (1993).
52. M. S. El Naschie. Average symmetry, stability and mean ergodicity of multidimensional Cantor sets, Il Nuovo Cimento 109B(2),149-157 (1994).
53. M. S. El Naschie. Statistical geometry of a Cantor discretum and semiconductors, Computers Math. Applic. 29(12),103-110 (1995).
54. M. S. El Naschie. Introduction to nonlinear dynamics, general relativity and the quantum, Chaos, Solitons and Fractals 8(5), vii-x (1997).
55. M. Buslev. Synergetics Chaos, Order, Self-organization, World Scientific, Singapore (1994).
56. C. J. Foot and A. M. Steane. Gregarious atoms, Nature 376, 213-214 (1995).
57. K, Burnett. An intimate gathering of Bosons, Science 269, 182-183 (1995).
58. P. McClintock. Exploding electron bubbles, Nature 383, 764-765 (1996).
59. E. H. Wichmann. Fundamental Constants. McGraw-Hill Book Company, New York (1967).
60. D. J. Gross. On the uniqueness of physical theories. In: De C. Tar, J. Finkelstein and C-I. A. Tan (eds.). Passion for Physics. World Scientific, Singapore (1985).
61. P. C. W. Davies. The Forces of Nature. 2nd Edn. Cambridge University Press, Cambridge (1986).
62. E. R. Harrison. The cosmic numbers, In The World of Physics Vol III, Jefferson Hane Weaver, Simon and Schuster, New York (1986).
63. R. Omnes. The Interpretation of Quantum Mechanics. Princeton University. Press, Princeton, NJ (1994).
64. S. Glasstone. Source Book on Atomic Energy. Litten educational publishing Inc. New York, U.S.A. (1967).
65. A. B. Lahanas and D. V. Nanapoulos. The road to no scale super gravity, Phys. Rep 145, pp. 139 (1987).
66. G. Fogleman. Quantum strings, J. Phys. 55(4) , 330-336 (1987).
67. E. Witten. The holes are defined by the string, Nature 383, 215-217 (1996).
68. D. Z. Albert. Bohm's alternative to quantum mechanics, Sci. Am. May, 32-39 (1994).
Figures
Figure 1. Wave-particle duality in atmospheric flows.
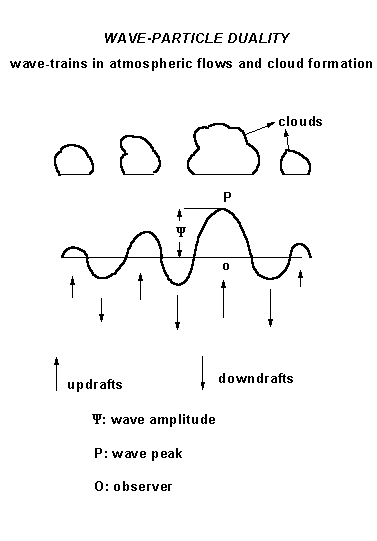
Figure 2. The quasiperiodic Penrose tiling pattern.

Figure 3. Instantaneous non-local connection in atmospheric eddy circulations.
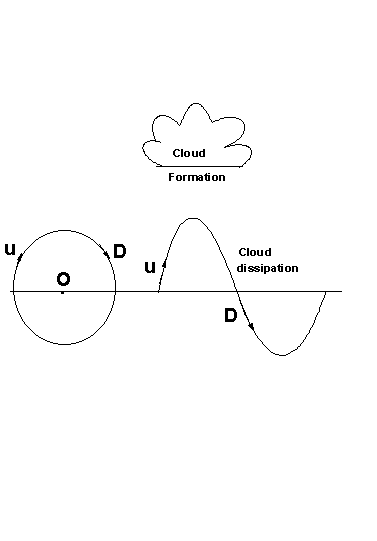
Table 1
Model predicted and statistical
normal probability density distributions
|
growth step |
normalized std dev |
probability densities |
|
|
n |
t |
model predicted P = t -4 t |
statistical normal distribution |
|
1 |
1 |
.1459 |
.1587 |
|
2 |
2 |
.0213 |
.0228 |
|
3 |
3 |
.0031 |
.0013 |