The complex spaciotemporal patterns of atmospheric flows that result from the cooperative existence of fluctuations ranging in size from millimetres to thousands of kilometres are found to exhibit long-range spacial and temporal correlations. These correlations are manifested as the self-similar fractal geometry of the global cloud cover pattern and the inverse power-law form for the atmospheric eddy energy spectrum. Such long-range spaciotemporal correlations are ubiquitous in extended natural dynamical systems and are signatures of deterministic chaos or self-organized criticality. In this paper, a cell dynamical system model for atmospheric flows is developed by consideration of microscopic domain eddy dynamical processes. This nondeterministic model enables formulation of a simple closed set of governing equations for the prediction and description of observed atmospheric flow structure characteristics as follows. The strange-attractor design of the field of deterministic chaos in atmospheric flows consists of a nested continuum of logarithmic spiral circulations that trace out the quasi-periodic Penrose tiling pattern, identified as the quasi-crystalline structure in condensed matter physics. The atmospheric eddy energy structure follows laws similar to quantum mechanical laws. The apparent wave-particle duality that characterize quantum mechanical laws is attributed to the bimodal phenomenological form of energy display in the bidirectional energy flow that is intrinsic to eddy circulations, e.g., formation of clouds in updrafts and dissipation of clouds in downdrafts that result in the observed discrete cellular geometry of cloud structure.
 

    Traditional mathematical models of dynamical systems, i.e., systems which evolve with time are based on Newtonian continuum dynamics and consist of nonlinear partial differential equations. The nonlinear partial differential equations do not have analytical solutions, and numerical solutions obtained using digital computers are found to exhibit sensitive dependence on initial conditions. This results in chaotic solutions, thereby giving rise to deterministic chaos (1-4). Such deterministic chaos was first identified in the computer realization of a simple mathematical model of atmospheric flows (5). Even simple nonlinear mathematical models are found to exhibit deterministic chaos, thereby imposing limits on the long-term predictability of the dynamical system, e.g., long-range weather prediction (6-11). Ruelle and Takens (12) were the first to identify an analogy between  deterministic chaos and turbulence, which is unpredictable, as modelled by the Navier-Stokes (NS) equations for fluid flows (13). There is now a growing conviction that traditional concepts of natural laws and their mathematical formulations in model continuum dynamical systems are inherently unstable for calculus-based long-term numerical computation schemes that use digital computers, which have inherent roundoff errors (14-16). There now exists a need for alternative concepts of natural laws that can be used to formulate simple analytical equations to model space-time continuum evolution of dynamical systems (17).
    Long-range spaciotemporal correlations, recently identified as self-organized criticality (18), are signatures of deterministic chaos (19) in real world dynamical systems, and they indicate sensitive dependence on initial conditions, i.e., microscopic scale dynamical laws govern the spaciotemporal evolution of the macroscale pattern. It has not yet been possible to idenify the laws governing the dynamics of evolution for the microscopic scale internal structure of the macroscale dynamical system that is characterized by a self-similar spatial pattern concomitant with long-range temporal corelations or 1/n noise. Such a self-organized robust spaciotemporal structure of the strange attractor with fractal pattern formation is a collective phenomenon resulting from the interaction of a large number of subsystems (19, 20). The mathematical concept of fractals characterizes objects on various scales, large as well as small, and thus reflects a hierarchical principle of organization. In this paper, a cell dynamical system model (21) for deterministic chaos in atmospheric flows is developed by consideration of microscopic domain eddy dynamical processes. The model enables formulation of scale-invariant governing equations for the observed atmospheric flow stucture characteristics (22-26). To begin with, a brief summary of the latest developments in the modelling of dynamical systems, in particular the concept of deterministic chaos, is presented in Sects. 2-4. In Sects. 5-7, the signature of deterministic chaos in the observed structure of atmospheric flows are identified, the limitations of existing numerical weather prediction models are discussed, and a cell dynamical system model for atmospheric flows is described. Finally, in Sect. 8 it is shown that the laws governing atmospheric flows are similar to quantum mechanical laws for subatomic dynamics. The model enables us to predict the following. (i) The strange-attractor design of fluid flows consists of a nested continuum of helical vortex-roll circulations with ordered two-way energy feedback between the larger and smaller scales. (ii) The microscopic scale internal structure of the overall logarithmic spiral vortex-roll circulations consist of the quasiperiodic Penrose tiling pattern identified as the quasi-crystalline structure in condensed matter physics (27). (iii) The atmospheric eddy energy structure follows laws similar to quantum mechanical laws.
 

    Mathematical models of dynamical systems, i.e., systems that evolve with time are traditionally formulated using Newtonian continuum dynamics where it is assumed that all change is continuous and the evolution equations of dynamical systems are given by a system of partial diferential equations representing continuous rate of change. The partial differential equations in general do not have analytical solutions and therefore numerical solutions are obtained using digital computers having finite precision. Such digital computer realizations of continuum mathematical models for dynamical systems are inherently unrealistic and result in deterministic chaos as explained earlier (Sect. 1). Mathematical studies by scientists in diverse disciplines have revealed the existence of deterministic chaos in disparate dynamical systems (1, 19, 28). The computed trajectory of the dynamical system in the phase space comprising the position and momenta coordinates traces out the self-similar fractal geometrical shape of the strange attractor, so named because of its strange convoluted shape being the final destination (attractor) of the trajectories. Any two initially close points in the strange attractor rapidly diverge with time and follow totaly different paths, though still within the strange-attractor domain. Therefore, the future trajectories of initially close points are unpredictable or random. The exact physical reason for the sensitive dependence on initial conditions of deterministic nonlinear partial differential, which are used for modelling dynamical systems as well as the self-similar fractal geometry of the strange-attractor design that characterizes  the evolution trajectory in the phase space of the dynamical system, is not yet identified (3, 4). Self-similarity implies scale invariance and is a manifestation of dilation symmetry, whereby the shape of an object is preserved during stretching. A self-similar object possesses the same internal structure on all scales. Such self-similar objects are non-Euclidean in shape and therefore possess a fractional or fractal dimension (29-31). The fractal dimension D is given by the relation D = d ln M/d ln R where M is the mass contained within a distance R from a fixed point in the object. The fractal dimension therefore gives in logarithmic scale the mass distribution per unit length along any direction in the extended object. When the fractal dimension is a constant for all length scales R, it indicates uniform stretching on a logarithmic scale or an inverse power-law form with constant exponent D for the mass distribution with respect to distance from a fixed point in the object. In general, objects in nature possess a multifractal structure, i.e., the fractal dimension is different for different length scales R (32).
 

    The computed strange attractor of dynamical systems is a mathematical artifact (15) as explained earlier and bears no relationship to the actual evolution trajectory. Further, even for a realistic mathematical model, computer roundoff errors introduce nontrivial uncertainities in the space differentials, namely dx, dy and dz that result in artificial curvature for the trajectory, which eventually ends up as limit cycles or periodicities for sufficiently long integration time periods. Computer precision therefore, plays the role of a yardstick in numerical model realizations and generates self-similar structures for the continuum phase space trajectory, namely the strange attractor.
    Recent studies show that numerical model results scale with computer precision, and periodicities in numerical model results are also a function of computer precision (14, 16). Computer model realizations that require long integration times are therefore subject to computer precision uncertainities that result in the loss of the predictability of the future state of the system.
    However, such sensitive dependence on initial conditions is actually exhibited by disparate real-world dynamical systems and may be associated with information transport from the microscale to the macroscale, which is indicated by the long-range spacial and temporal correlations intrinsic to such systems. Therefore, microscopic scale differences in initial conditions may contribute to appreciably different large-scale space-time structures. It is important to identify the exact microscopic scale mechanisms that contribute to the macroscale space-time evolution of the robust self-similar strange-attractor design. It should be possible to identify a simple conceptual model that is scale invariant for the dynamical evolution of the system, i.e., a microscopic scale scale unit-cell model that is directly applicable to the macroscale multicellular model. Such a model for atmospheric flows is described in Sect.7 and enables formulation of the dynamical processes of evolution in simple mathematical formulations with analytical (algebraic) solutions or where the numerical solutions does not require long-term integration using digital computers.
 

    In this nondeterministic computational technique, the dynamical system is assumed to consist of an assembly of identical unit cells. Starting with arbitrary initial conditions, the evolution of the dynamical system proceeds at successive unit length steps during unit intervals of time following arbitrary laws of interaction between adjacent cells. The 'cellular automata' belong to the cell dynamical system described above and do not require calculus-based long-term integration schemes (21). However, the cellular-automata rules for evolution are arbitrary and do not have any physical basis. The relevant physical processes must therefore be incorporated in the cellular-automata schemes. A cellular-automata computational scheme that incorporates the physics of atmospheric flows is described in Sect. 7.
 

    Recent advances in remote sensing and in situ measurement techniques have enabled us to document the following new observational characteristics of turbulent shear flows in the planetary atmospheric boundary layer (ABL) where weather activity occurs. The ABL extends to about 10 km above the surface of the earth.
    (i) The atmospheric flow consists of a full continuum of fluctuations ranging in size from the turbulence scale of a few millimetres to the planetary scale of thousands of kilometres.
    (ii) The atmospheric eddy energy spectrum follows an inverse power law of form n ^-B , where n is the frequency and B the exponent. The exponential power-law form for the eddy energy spectrum indicates self-similarity and scale invariance. The exponent B is found to be equal to 1.8 for both meteorological (time period in days) and climatological (time period in years) scales, which indicates a close coupling between the two scales (33-39).
    (iii) Satellite cloud-cover photographs give evidence for the existence of helical vortex-roll circulations (or large eddies) in the ABL as indicated by the organization of clouds in rows and (or) streets, mesoscale (up to 100km) cloud clusters (MCC), and spiral bands in synoptic scale weather systems (40).
    (iv) The structure of atmospheric flows is invariably helical (curved) as manifested in the visible cloud patterns of weather systems, e.g., all basic mesoscale structures such as medium scale tornado generating storms, squall lines, hurricanes, etc. (41), and in particular the supercell storm (42).
    (v) Atmospheric flows give an implicit indication of the upscale transfer of a certain amount of energy inserted at much smaller scales, thereby generating the observed helical fluctuations (41, 43).
    (vi) The global cloud-cover pattern exhibits self-similar fractal geometrical structure and is consistent with the observed scale invariance of the atmospheric eddy energy spectrum (35, 44) (see characteristic (ii) above).
    Atmospheric weather systems exist as coherent structures consisting of discrete cloud cells forming patterns of rows and (or) streets, MCC, and spiral bands. These patterns maintain their identity for the duration of their appreciable lifetimes in the apparently dissipative turbulent shear flows of the ABL (45). The existence of coherent structures (seemingly systematic motion) in turbulent flows, in general, has been well established during the last 20 years of research into turbulence. However, it is still debated whether these structures are the consequences of some kind of instabilities (such as shear or centrifugal instabilities), or whether they are manifestations of some intrinsic universal properties of any turbulent flow (41).
    Lovejoy and Schertzer (35) have provided conclusive evidence for the signature of deterministic chaos in atmospheric flows, namely the fractal geometry of global cloud-cover pattern and the inverse power-law form n ^-B where n is the frequency and B the exponent for the atmospheric eddy energy spectrum. Atmospheric teleconnections, such as the El Nino and (or) Southern Oscillation (ENSO) cycles in weather patterns, that are responsible for devastating changes in normal global weather regimes (46-48) are also manifestations of long-range correlations in regional weather activity. ENSO is an irregular (2-5 years), self-sustaining cycle of alternating warm and cool water episodes in the Pacific Ocean. Also called El-Nino - La Nina, La Nina refers to the cool part of the weather cycle while El-Nino is associated with a reversal of global climatic regimes resulting in anomalous floods and droughts throughout the globe.

    Presently available models for ABL turbulent flows are incapable of identifying the coherent helical structural form intrinsic to turbulence. Also, the models do not give realistic simulations of the space-time averages for the thermodynamic parameters and the fluxes of buoyant energy, mass, and momentum because of the following inherent limitations.
    (i) The physics of the observed coherent helical geometric structure inherent in turbulent flows is not yet identified, and therefore the structural form of turbulent flows cannot be modelled.
    (ii) By convention, the Newtonian continuum dynamics of the atmospheric flows are simulated by the NS equations which are inherently nonlinear, and being sensitive to initial conditions, give chaotic solutions characteristic of deterministic chaos.
    (iii) The governing equations do not incorporate the mutual coexistence and interaction of the full spectrum of atmospheric fluctuations that form an integral part of atmospheric flows (10, 36, 49, 50).
    (iv) The limitations of available computer capacity necessitate severe truncations of the governing equations, thereby generating errors of approximations.
    (v) The above-mentioned uncertainties are further magnified exponentially with time by computer roundoff errors and result in unrealistic solutions (14, 15). Recent exhaustive studies by Weil (51) and others also indicate that existing numerical models of atmospheric boundary layer flows require major revisions to incorporate an understanding of turbulence and diffusion in boundary layer flows. Recently, there has been growing conviction that curent numerical weather prediction models are inadequate for accurate forecasts (16, 52-55). Numerical modelling of atmospheric flows, diffusion, and cloud growth therefore require alternative concepts and computational techniques.
 

6.1    Deterministic chaos and weather prediction: current status

    At present, the signatures of deterministic chaos, namely the fractal geometrical structure concomitant with 1/n noise, have been conclusively identified in model and real atmospheric flows, and the fractal dimension of the strange attractor traced by atmospheric flows has been estimated with recently developed numerical algorithms (55), which use the time series data of meteorological parameters, e.g., rainfall, temperature, windspeed, etc. However, such estimations of the fractal dimension have not helped resolve the problem of the formulation of a simple closed set of governing equations for atmospheric flows (57-60) mainly because the basic physics of deterministic chaos is not yet identified.
 

    The nondeterministic model described below incorporates the physics of the growth of macroscale coherent structures from microscopic domain fluctuations in atmospheric flows. In summary, the mean flow at the planetary ABL posesses an inherent upward momentum flux of frictional origin at the planetary surface. This turbulence-scale upward momentum flux is progressively amplified by the exponential decrease of the atmospheric density with height coupled with the buoyant energy supply by microscale fractional condensation on hygroscopic nuclei, even in an unsaturated environment (61). The mean large-scale upward momentum flux generates helical vortex-roll (or large eddy) circulations in the planetary atmospheric boundary layer and is manifested as cloud rows and (or) streets, and MCC in the global cloud cover pattern. A conceptual model of large and turbulent eddies is shown in Fig. 1.

    FIG 1. Conceptual model of large and turbulent eddies in the planetary ABL. The mean air flow at the planetary surface carries the signature of the fine scale features of the planetary surface topography as turbulent fluctuations with a net upward momentum flux. This persistent upward momentum flux of surface frictional origin generates large-eddy (or vortex-roll) circulations, which carry upward the turbulent eddies as internal circulations. Progressive upward growth of a large eddy occurs because of buoyant energy generation in turbulent fluctuations as a result of the latent heat of condensation of atmospheric water vapour on suspended hygroscopic nuclei such as common salt particles. The latent heat of condensation generated by the turbulent eddies forms a distinct warm envelope or a microscale capping inversion layer at the crest of the large-eddy circulations as shown in the upper part of the figure. The lower part of the figure shows the progressive upward growth of the large eddy from the turbulence scale at the planetary surface to a height R and is seen as the rising inversion of the daytime atmospheric boundary layer. The turbulent fluctuations at the crest of the growing large-eddy mix overlying environmental air into the large-eddy volume, i.e., there is a two-stream flow of warm air upward and cold air downward analogous to superfluid turbulence in liquid helium (see ref. 79). The convective growth of a large eddy in the atmospheric boundary layer therefore occurs by vigorous counter flow of air in turbulent fluctuations (see also Fig. 4), which releases stored buoyant energy in the medium of propagation, e.g., latent heat of condensation of atmospheric water vapour. Such a picture of atmospheric convection is different from the traditional (see ref. 78) concept of atmospheric eddy growth by diffusion, i.e., analogous to the molecular level momentum transfer by collision.

The generation of turbulent buoyant energy by the microscale fractional condensation is maximum at the crest of the large eddies and results in the warming of the large-eddy volume. The turbulent eddies at the crest of the large eddies are identifiable by a microscale capping inversion that rises upward with the convective growth of the large eddy during the course of the day. This is seen as the rising inversion of the daytime planetary boundary layer in echosonde and radiosonde records and has been identified as the entrainment zone (62) where mixing with the environment occurs.
    Townsend (63) has investigated the structure and dynamics of large-eddy formations in turbulent shear flows and has shown that large eddies of appreciable intensity form as a chance configuration of turbulent motion as illustrated in the following example. Consider a large eddy of radius R that forms in a field of isotropic turbulence with turbulence length and velocity scales 2r and w_* , respectively. The dominant turbulent eddy radius is therefore equal to w_* . The mean square circulation C² at any instant around a circulation path of large-eddy radius  R is given by
 

where w_* is tangential to the path elements ds and the motions in sufficiently separated parts of the flow are statistically independent. The mean-square velocity of circulation W ² in the large eddy of radius R is given by
 

The above equation enables us to compute the instantaneous acceleration dW for a large-eddy of radius R generated by the spatial integration of the inherent dominant turbulence-scale vertical acceleration  w_*  of length scale 2r . The large-eddy growth from turbulence scale fluctuations may be visualized as follows. The large-eddy domain is defined by the overall envelope of the turbulent fluctuations, and incremental growth of the large-eddy occurs in discrete length steps equal to the turbulent outward displacement of air parcels. Such a concept outlined above for large-eddy growth from turbulence scale buoyant energy generation envisages large-eddy growth in discrete length step increments dR equal to r and is therefore analogous to the cellular automata computational technique (see Sect. 4) where cell dynamical system growth occurs in unit length steps during unit intervals of time, the turbulence scale yardsticks for length and time being used for measuring large-eddy growth. A continuous spectrum of progressively larger eddies are thus generated in the ABL. Large-eddy growth by such successive length scale doubling is hereby identified as the universal period doubling route to the chaotic eddy growth process. Therefore, the turbulent eddy acceleration  w_* generates, at any instant, the large-eddy incremental growth dR  associated with large-eddy incremental acceleration dW  as given by [1] as
 

Equation [1] signifies a two-way ordered energy (kinetic energy) flow between the smaller and larger scales and [1] is therefore identified as the statement of the law of conservation of energy for the universal period doubling route for chaos eddy growth processes in atmospheric flows. Figure 2 shows the concept of the universal period doubling route for chaotic eddy growth process by the self-sustaining process of ordered energy feedback between the larger and smaller scales, the smaller scales forming the internal circulations of the larger scales.

     FIG 2.   Physical concept of the universal period doubling route to chaotic eddy growth process by the self-sustaining process of ordered energy feedback between the larger and smaller scales, the smaller scales forming the internal circulations of the larger scales. The figure shows a uniform distribution of dominant turbulent scale eddies of length scale 2r . Large-eddy circulations such as ABCD form as coherent structures sustained by the enclosed turbulent eddies. The r.m.s. circulation speed of the large eddy is equal to the spatially integrated mean of the r.m.s. circulation speeds of the enclosed turbulent eddies. Such a concept envisages large-eddy growth in unit length step increments during unit intervals of time with turbulence-scale yardsticks for length and time, and is therefore analogous to the cellular automata computational technique. The growth of the large-eddy by successive period doubling, namely, discrete length step increments equal to the turbulence length scale is identified as the physics of the universal period doubling route to chaos eddy growth process.
 

Atmospheric boundary layer flows, therefore, generate, as a natural consequence of surface friction, persistent microscopic domain turbulent fluctuations that amplify and propagate upward and outward spontaneously as a result of the buoyant energy supply from the latent heat of condensation of atmospheric water vapour on suspended hygroscopic nuclei in the upward fluctuations of air parcels. The evolution of the macroscale atmospheric eddy continuum structure occurs in successive microscopic fluctuation length steps in the ABL and therefore has a self-similar scale-invariant fractal geometrical structure by concept and also according to [1]. Equation [1] is therefore identified as the universal algorithm that defines the space-time continuum evolution of the atmospheric eddy energy structure (strange attractor). Such a concept of the autonomous growth of the atmospheric eddy continuum with ordered energy flow between the scales is analogous to the 'bootstrap' theory of Chew (64), the theory of implicate order envisaged by Bohm (65), and Prigogine's concept of the spontaneous emergence of order through a process of self-organization (65).
    The turbulent eddy circulation speed and radius increase with the progressive growth of the large eddy as given in [1]. The successively larger turbulent fluctuations, which form the internal structure of the growing large eddy, may be computed from [1] as
 

During each length step growth dR , the small-scale energizing perturbation W_n at the n^th instant generates the large-scale perturbation W_n+1 of radius R  where R = S₁ⁿ dR  since successive length-scale doubling gives rise to R . Equation [3] may be written in terms of the successive turbulent circulation speeds W_n and W_n+1 as

[4]

The angular turning dq inherent to eddy circulation for each length step growth is equal to dR/R . The perturbation dR  is generated by the small-scale acceleration W_n at any instant n and therefore dR = W_n . Starting with the unit value for dR  the successive W_n, W_n+1 , R , and dq values are computed from [4] and are given in Table 1.

It is seen that the succesive values of the circulation speed W and radius R  of the growing turbulent eddy follow the Fibonacci mathematical number series such that R_n+1 = R_n + R_n-1 and R_n+1/R_n is equal to the golden mean t , which is equal to [(1 +sqrt(5))/2] ~ (1.618). Further, the successive W  and R  values form the geometrical progression R₀(1 + t + t² + t³ + t⁴ + ....) where R₀ is the initial value of the turbulent eddy radius.

(a)

 FIG. 3.    The internal structure of large-eddy circulations. (a) Turbulent eddy growth from primary perturbation OR_o starting from the origin O gives rise to compensating return circulations OR₁R₂  on either side of OR_o , thereby generating the large eddy radius OR₁ such that OR₁/OR_o = t and R_oOR₁ = p/5 = R_oR₁O. Five such successive length step growths give successively increasing radii OR₁ , OR₂ , OR₃ , OR₄ and OR₅ tracing out one complete vortex-roll circulation such that the scale ratio OR₅/OR_o is equal to t⁵ = 11.1. The envelope R₁R₂R₃R₄R₅  of a dominant large eddy (or vortex roll) is found to fit the logarithmic spiral R = R_o e^bq where R_o = OR_o , b= tan a with a the crossing angle equal to p/5, and the angular turning q for each length step growth is equal to p/5. (b) The logarithmic spiral R = R_o e^bq is drawn as OAB for clarity. The successively larger eddy radii may be subdivided again in the golden mean ratio. (c) The internal structure of large-eddy circulations is, therefore, made up of balanced small-scale circulations, which trace out the well-known quasiperiodic Penrose tiling pattern identified as the quasi-crystalline structure in condensed matter physics. Therefore, short-range circulation balance requirements generate successively larger circulation patterns with precise geometry governed by the Fibonacci mathematical number series and is identified as the signature of the universal period doubling route to chaos in atmospheric flows.
 

Turbulent eddy growth from primary perturbation OR_o starting from the origin O (Fig. 3) gives rise to compensating return circulations OR₁R₂  on either side of OR_o , thereby generating the large eddy radius OR₁ such that OR₁/OR_o = t and R_oOR₁ = p/5 = R_oR₁O. Therefore, short-range circulation balance requirements generate successively larger circulation patterns with precise geometry that is governed by the Fibonacci mathematical number series, which is identified as a signature of the universal period doubling route to chaos in fluid flows, in particular atmospheric flows. It is seen from Fig. 3 that five such successive length step growths give successively increasing radii OR₁ , OR₂ , OR₃ , OR₄ and OR₅ tracing out one complete vortex-roll circulation such that the scale ratio OR₅/OR_o is equal to t⁵ = 11.1. The envelope R₁R₂R₃R₄R₅ (Fig. 3) of a dominant large eddy (or vortex roll) is found to fit the logarithmic spiral R = R_o e^bq where R_o = OR_o , b= tan a with a the crossing angle equal to p/5, and the angular turning q for each length step growth is equal to p/5. The successively larger eddy radii may be subdivided again in the golden mean ratio. The internal structure of large-eddy circulations is, therefore, made up of balanced small-scale circulations tracing out the well-known quasiperiodic Penrose tiling pattern identified as the quasi-crystalline structure in condensed matter physics. A complete description of the atmospheric flow field is given by the quasi-periodic cycles with Fibonacci winding numbers. The self-organized large-eddy growth dynamics, therefore, spontaneously generate an internal structure with the fivefold symmetry of the dodecahedron, which is referred to as the icosahedral symmetry, e.g., the geodesic dome devised by Buckminster Fuller. Incidentally, the pentagonal dodecahedron is, after the helix, nature's second favourite structure (67). Recently, a carbon macromolecule C₆₀ , formed by condensation from a carbon vapour jet, was found to exhibit the icosahedral symmetry of the closed soccer ball and has been named Buckminsterfullerene or footballene (68, 69). It may be noted that it has not been possible to create such  C₆₀ Buckminsterfullerene molecules by traditional chemical reaction methods. Such a quasi-crystalline structure has recently been identified in numerical simulation of fluid flows (70).
    The time period of large-eddy circulation made up of internal circulations with the Fibonacci winding number is arrived at as follows. Assuming turbulence-scale yardsticks for length and time, the primary turbulence-scale perturbation generates successively larger perturbations with the Fibonacci winding number on either side of the initial perturbation. Therefore, the large-eddy time period T  is directly proportional to the total circulation path traversed on any one side, and is given in terms of the turbulence scale time period t as

[5]      T = t [ 2 (1 + t +t² + t³+ t⁴ ) + t⁵ ] = 43.74 t

Therefore, the large-eddy circulation time period is also related to the geometrical structure of the flow pattern.

7.1    Dominant weather cycles (limit cycles)

    It was shown above that dominant large-eddy growth occurs from turbulence-scale energy pumping for successive scale ratio ranges t⁵ = 11.09 .Therefore, from [1] the following relations are derived for the length and time scales of limit cycles in atmospheric flows.

    The limit cycles or dominant periodicities in atmospheric flows (71), possibly originating from solar-powered primary oscillations, are given in the following. (i) The 40- to 50-day oscillation in the atmospheric general circulation and the quasi-five yearly ENSO phenomena (49) may possibly arise from diurnal surface heating. (ii) The 40- to 50-year cycle in climate may be a direct consequence of the annual solar cycle (summer and winter oscillation). (iii) The quasi-biennial oscillation (QBO) in the tropical stratospheric wind flows may arise as a result of the semidiurnal pressure oscillation. (iv) The 22-year cycle in weather patterns associated with the solar sunspot cycle may be related to the newly identified 5-min oscillations of the sun's atmosphere (72). The growth of large eddies by energy pumping at smaller scales, namely the diurnal surface heating, the semidiurnal pressure oscillation, and the annual summer-winter cycles as cited above is analogous to the generation of chaos in optical emissions triggered by a laser pump (73). Recent barometer data on the planet Mars, whose tenuous atmosphere magnifies atmospheric oscillations, reveal oscillations with periods very close to 1.5 Martian days preceding episodes of global dust storms (74), which indicates a possible cause and effect mechanism as given in [6]. The identification of limit cycles in atmospheric flows is possible by means of the continuous periodogram analysis of long-term high-resolution surface pressure data and this will help long-term prediction of regional atmospheric flow pattern (75).
    As seen from Fig. 3 and from the concept of eddy growth, vigorous counter flow (mixing) characterizes the large-eddy volume. the steady-state fractional volume dilution k of the large-eddy volume by environmental mixing is given by

Earlier it was shown that the successive eddy length step growths generate the angular turning dq of the large-eddy radius R given by dR/R, which is a constant equal to 1/t where t is the golden mean. Further, the successive values of the r.m.s. circulation speed W and the corresponding radius R of the large eddy follow the Fibonacci mathematical number series. Therefore, the value of k , the steady state volume dilution of the large eddy by the turbulent eddy fluctuations for each length step growth of the large eddy, is found from [7] to be

[8]                              k = 1/t²= 0.382

Since the steady-state fractional volume dilution of the large eddy by inherent turbulent eddy fluctuations during successive length step increments is equal to 0.382, i.e., less than half, the overall Euclidean geometrical shape of the large eddy is retained as manifested in the cloud billows, which resemble spheres.
    The fractional outward mass flux of air across a unit cross section for any two successive steps of eddy growth is given by

f_c is therefore equal to the percolation threshold for critical phenomena, i.e., where the liquid-gas mixture separates into the liquid and gas phases with the formation of self-similar fractal structures (76) and in the case of atmosphereric flows this is associated with the manifestation of coherent vortex-roll structures. The ratio of the actual (observed) cloud liquid water content q to the adiabatic liquid water content q_a , i.e., without mixing with the environment, is found to be less than one and has been attributed to the mixing of the environmental air into the cloud volume. The measured value of q/q_a at the cloud base is found to be 0.61 (77) in agreement with that predicted by f_c above; it is also consistent with the observed fractal geometry of cloud shape.
    The vigorous counterflow of air (mainly vertically) in turbulent eddy fluctuations characterizes the internal structure of the growing large eddy. The turbulent eddies carried upward by the growing large eddy are amplified to form 'cloud-top gravity oscillations' and are manifested as the distictive cauliflower-like surface granularity of the cumulus cloud growing in the large-eddy updraft regions under favourable conditions of moisture supply (Fig. 4). Therefore, atmospheric convection and the associated mass, heat, and momentum transport in the ABL occur by the vigorous counterflow of air in intrinsic fractal structures and not by eddy diffusion processes postulated by the conventional theories of atmospheric convection (78). Such a concept of atmospheric convection is analogous to superfluid turbulence in liquid helium (79).

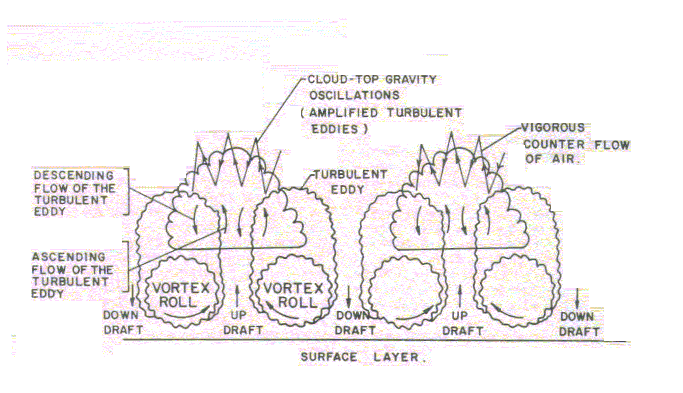
    FIG. 4. Cloud structure in the ABL. The turbulent eddies carried upward by the growing large eddy (see Fig. 1) are amplified to form cloud-top gravity (buoyancy) oscillations and are manifested as the distinctive cauliflower-like surface granularity of the cumulus cloud growing in the large-eddy updraft regions under favourable conditions of moisture supply in the environment. The fractal or broken cloud structure is a direct result of cloud water condensation and evaporation, respectively, in updrafts and downdrafts of the innumerable microscale turbulent eddy fluctuations in the cloud volume. Therefore, atmospheric convection and the associated mass, heat, and momentum transport in the ABL occur by the vigorous counterflow of air in intrinsic fractal structures and not by eddy diffusion processes postulated by the conventional theories of atmospheric convection (see Fig. 1).

The above equation is the well-known logarithmic spiral relationship for wind profile in the surface ABL derived from conventional eddy diffusion theory (78) where k is a constant of integration and its magnitude is obtained from observations as 0.4 (80). The logarithmic wind-profile relationship is consistent with the overall logarithmic flow structure pattern of the quasi- periodic Penrose tiling pattern that is traced by atmospheric flows as was deduced earlier and shown in Fig. 3. The cell dynamical system model for atmospheric flows enables us to predict the logarithmic spiral profile for the wind for the entire ABL . Further, the value of the Von Karman's constant k is obtained as equal to 0.382, as a natural consequence of environmental mixing during dominant large-eddy growth, and is in agreement with observations. Von Karman's constant is therefore identified as the universal constant for deterministic chaos in the real world dynamical system of atmospheric flows. The predicted logarithmic spiral trajectory for ABL flows is seen markedly in the hurricane spiral pattern. Such coherent helicity is intrinsic to atmospheric flows (41).
 

    Historically, macroscale physical phenomena are described by classical dynamical laws (Newton's laws) for all practical purposes, while subatomic phenomena, e.g., electromagnetic radiation require quantum mechanical laws to explain their physical manifestation. It has not yet been possible to identify a universal theory of everything (TOE) for the totality of manifested phenomena from the macro- to the subatomic scales. So far classical dynamical laws have failed to explain deterministic chaos in macroscale dynamical systems. On the other hand, the standard interpretation of quantum mechanics, chiefly the ad hoc assumption of the wave-particle duality for the quantum system, e.g., electron or photon, does not provide a complete description of a quantum system. Though quantum mechanical laws are successful in describing subatomic phenomena, the following inconsistencies are yet to be resolved.
    (i) The interpretation of Shrodinger's wave function as quantities whose squared amplitudes give the probability density that a particle will be at a particular place (if the arguments of the wave function are in space coordinates). Such a declaration that algebraically additive amplitudes must be squared to obtain probability densities is unsatisfactory in the absence of physically consistent mathematically rigorous proof (81).
    (ii) The unresolved issue of nonlocality in quantum mechanics, namely, the Einstein-Podolsky-Rosen (EPR) 'paradox', whereby the spatially separated parts of a quantum system (photon, electron, etc.) respond as a unified whole to local perturbations (84, 85).
    (iii) Energy propagation and interchange in quantum systems occur in discrete quanta or packets of energy content hn where h  is a universal constant of nature (Planck's constant) and n is the frequency in cycles per second of the electromagnetic radiation. The exact physical mechanism responsible for the manifestation of subatomic phenomena as discrete packets of energy propagating as waves, i.e., the wave-particle duality is not yet identified.
    (iv) Finally, quantum mechanical laws, which govern the ultimate structure of matter, cannot be interpreted in terms of macroscale real world phenomena.
    In the following it is shown that atmospheric flow structure follows laws similar to quantum mechanical laws for subatomic dynamics. The apparent inconsistencies of quantum mechanical laws described above are explained in terms of the physically consistent characteristics inherent in eddy circulation patterns in atmospheric flows.
    In summary: the kinetic energy (KE) of an eddy of rotation frequency n , angular speed w = 2pn , r.m.s. circulation speed W_p, and radius R_p in the hierarchical eddy continuum is equal to pHn , where H   is the angular momentum of the largest eddy of mass M  in the hierarchy. The r.m.s. circulation speed of the largest eddy in the continuum is equal to the integrated mean of all the inherent turbulent eddy circulations (Sect. 7).

From [1],

Furthermore,

KE = pHn = (1/2)Hw

H is equal to the product of the momentum of the planetary scale eddy and its radius and therefore represents the angular momentum of the planetary scale eddy about the eddy centre. Therefore, the KE of any component eddy of frequency n of the scale invariant eddy continuum is equal to pHn . Further, since the large eddy is but the sum total of the smaller scales, the large eddy energy content is equal to the sum of all its individual component eddy energies and therefore the KE energy distribution is normal and the KE of any eddy of radius R in the eddy continuum, expressed as a fraction of the energy content of the largest eddy in the hierarchy, will represent the cumulative normal probability density distribution. The eddy continuum energy spectrum is therefore the same as as the cumulative normal probability density distribution plotted on a log-log scale and the eddy energy probability density distribution is equal to the square of the eddy amplitude. Therefore, the atmospheric eddy continuum energy structure follows laws that are similar to quantum mechanical laws without exhibiting any of the apparent inconsistencies of the quantum mechanical laws for subatomic dynamics as illustrated in Fig. 5 and explained in the following.

    FIG. 5. Quantum mechanical analogy with macroscale phenomena of atmospheric flows. The upper part of the figure illustrates the concept of wave-particle duality as physically consistent in the common place observed phenomena of the formation of clouds in a row as a natural consequence of cloud formation and dissipation, respectively, in the updrafts and downdrafts of vortex roll circulations in the ABL. The lower part of the figure illustrates the concept of non-locality by analogy with instantaneous transfer of energy from effort to load in a pulley and as also inferred by the physically consistent phenomena of instantaneous circulation balance in the atmospheric vortex-roll circulations with alternating balanced high- and low-pressure areas.

    The nondeterministic cell dynamical system model for atmospheric flows described in this paper enables us to formulate simple analytical (algebraic) equations for the atmospheric flow structure pattern, i.e., the strange attractor, and to predict the following new results.
    (i) The strange-attractor design of atmospheric flow structure consists of a nested continuum of vortex-roll circulations with ordered energy flow between the scales.
    (ii) Large-eddy circulations grow from space-time integration of internal nontrivial small-scale energy pumping, e.g., solar-powered turbulent buoyant energy of frictional origin in atmospheric flows. Therefore, small-scale circulation balance requirements impose long-range orientational order and are manifested as the quasi-periodic Penrose tiling design for the internal structure of large-eddy circulations with overall logarithmic spiral flow pattern. The growth of large eddies by successive unit length step increments equal to the turbulence-scale length is identified as the universal period doubling route to a chaotic eddy growth process in atmospheric flows.
    (iii) The universal constant for deterministic chaos is identified as Von Karman's constant and is equal to 0.382, which quantifies the steady state fractional volume dilution of large eddies by turbulent fluctuations.
    (iv) Convective growth of large eddies in atmospheric flows occurs by vigorous counterflow in inherent tubulent eddy fluctuations and not according to the conventional concept of eddy diffusion, i.e., momentum transfer by collision. Such a concept is analogous to superfluid turbulence in liquid helium.
    (v) Atmospheric flows follow laws similar to quantum mechanical laws. The quantum mechanical analogy with macroscale atmospheric flows is seen in  commonplace events such as the formation of clouds at the crests (updrafts) of eddy (wave) circulations, e.g., clouds in a row, thereby resolving the apparent paradox of wave-particle duality.
    Since the strange attractor design of atmospheric flow structure consists of periodicities with fine structure (continuum) a continuous periodogram analysis of time series data will enable a complete description of the strange attractor and such a concept has recently been put forth by Cvitanovic (85). Further, identification of dominant periodicities, i.e., limit cycles in atmospheric flows by continuous periodogram analyses of multistation high-resolution surface pressure data may help long-range (months to years) forecasts of global weather patterns.
 
 

1.    W. FAIRBAIRN, Phy. Bull. 37, 300 (1986).
2.    J. GLEICK, Chaos: making a new science. Viking Press Inc., New York,
       1987, pp. 1-252.
3.    R. POOL, Science (Washington, D.C.), 245, 26 (1989).
4.    I. PERCIVAL, New Sci. 118, 42 (1989).
5.    E. N. LORENZ, J. Atmos. Sci. 20, 130 (1963).
6.    E. N. LORENZ, J. Atmos. Sci. 36, 1367 (1979).
7.    E. N. LORENZ, J. Meteorol. Soc. Jpn. 60, 255 (1982).
8.    E. N. LORENZ, Tellus, Series A: Dynamic Meteorology and
       Oceanography 36, 98 (1984).
9.    E. N. LORENZ, In Predictability of fluid motions. Edited by G. Holloway
       and B. J. West. Amer. Inst. Phys., New York, 1984, pp. 133-139.
10.  E. N. LORENZ, In Perspectives in nonlinear dynamics. Edited by M. F.
       Shlesinger, R. Crawley, A. W. Saenz, and W. Zachary, World
       Scientific,  Singapore, 1986, pp. 1-17.
11.  H. TENNEKES, In Turbulence and predictability in geophysical fluid
       dynamics and climate dynamics. Edited by M. Ghil, R. Benzi and G.
       Parisi, Ital. Phys. Soc., North Holland Pub. Co. Amsterdam, 1985, pp.
       45-70.
12.  D. RUELLE and F. TAKENS, Commun. Math. Phys. 20, 167 (1971).
13.  J. M. OTTINO, C. W. LEONG, H. RISING, and P. D. SWANSON, Nature
       (London), 333, 419 (1988).
14.  C. BECK and G. ROEPSTORFF, Physica D:  (Amsterdam), 25, 173 (1987).
15.  J. L. MCCAULEY, Phy. Scr. T, 20, 1 (1988).
16.  C. GREBOGI, E. OTT, and J. A. YORKE, Phys. Rev. A: Gen. Phys. 38,
       3688 (1988).
17.  P. DAVIES, New. Sci. 117, 50 (1988).
18.  P. C. BAK, C. TANG, and K. WIESENFELD, Phys. Rev. A: Gen. Phys. 38,
       364 (1988).
19.  I. PROCACCIA, Nature (London), 333, 618 (1988).
20.  P. COULLET, C. ELPHICK, and D. REPAUX, Phys. Rev. Lett. 58, 431
       (1987).
21.  Y. OONA and S. PURI, Phys. Rev. A: Gen. Phys. 38, 434 (1988).
22.  A. M. SELVAM, Proceedings of the National Aerospace and Electronics
       Conference (NAECON), USA, May 1987, IEEE, New York, 1987.
23.  A. M. SELVAM, Proceedings of the 8th Conference on Numerical
       Weather Prediction, USA, Feb. 1988. Published by American
       Meteorological Society, Baltimore, MD, USA, 1988.
24.  A. M. SELVAM, J. Lumin. 40 & 41, 535 (1988).
25.  A. M. SELVAM, Proceedings of the 1989 International Conference on
       Lightning and Static Electricity, University of Bath, UK, Sept. 1989.
26.  P. SIKKA, A. M. SELVAM, and A. S. RAMACHANDRA MURTY, Adv. Atmos.
       Sci. 2, 218 (1988).
27.  T. JANSSEN, Phys. Rep. 168, 1 (1988).
28.  A. A. CHERNIKOV and G. M. ZASLAVSKY, Phys. Today, 41, 27 (1988).
29.  B. B. MANDELBROT, Pure Appl. Geophys. 131, 5 (1989).
30.  C. FOIAS and R. TEMAM, Physica D: (Amsterdam), 32, 163 (1988).
31.  G. MAYER-KRESS, Phys. Bull. 39, 357 (1988).
32.  H. E. STANLEY and P. MEAKIN, Nature (London), 335, 405 (1988).
33.  E. M. DEWAN and R. E. GOOD, J. Geophys. Res. (Atmos.), 91, 2742
       (1986).
34.  T. E. VAN ZANDT, Geophys. Res. Lett. 9, 575 (1982).
35.  S. LOVEJOY and D. SCHERTZER, Bull. Amer. Meteorol. Soc. 67, 21
       (1986).
36.  D. C. FRITTS and H. G. CHOU, J. Atmos. Sci. 44, 3610 (1987).
37.  F. G. CANAVERO and F. EINAUDI, J. Atmos. Sci. 44, 1589 (1987).
38.  E. M. DEWAN, N. GROSSBARD, R. E. GOOD, and J. BROWN, Phys. Scr.,
       37, 154 (1988).
39.  T. TSUDA, T. INOUE, D. C. FRITTS, T. E. VAN ZANDT, S. KATO, T. SATO,
       and S. FUKAO, J. Atmos. Sci. 46, 2440 (1989).
40.  L. EYMARD, J. Atmos. Sci. 42, 2844 (1985).
41.  E. LEVICH, Phys. Rep. 3 & 4, 129 (1987); 151, 129 (1987).
42.  D. K. LILLY, J. Atmos. Sci. 43, 126, (1986).
43.  D. K. LILLY, J. Atmos. Sci. 46, 2026, (1989).
44.  D. SCHERTZER and S. LOVEJOY, Pure Appl. Geophys., 130, 57 (1989).
45.  H. TENNEKES, In Workshop on micrometeorology, Edited by D. A.
       Haughen, Amer. Meteorol. Soc. Boston, USA, 1973, pp.175-216.
46.  K. E. TRENBERTH, G. W. BRANSLATOR, and P. A. ARKIN, Science
       (Washington, D. C.), 242, 1640 (1988).
47.  Y. KUSHNIR and J. M. WALLACE, J. Atmos. Sci. 46, 3122 (1989).
48.  K. M. LAU, LI PENG, C. H. SUI, and TETSUO NAKAZWA, J. Meteorol. Soc.
       Jpn 67, 205 (1989).
49.  S. SHAFFEE and S. SHAFFEE, Phys. Rev. A: Gen. Phys. 35, 892 (1987).
50.  T. G. SHEPHERD, J. Atmos. Sci. 44, 1166 (1987).
51.  J. C. WEIL, J. Climat. Appl. Meteorol. 24, 1111 (1985).
52.  J. LIGHTHILL, Proc. R. Soc. London, A 407, 35 (1986).
53.  B. J. MASON, Proc. R. Soc. London, A 407, 51 (1986).
54.  B. REINHOLD, Science (Washington, D. C.), 235, 437 (1987).
55.  R. A. KERR, Science (Washington, D. C.), 244, 1137 (1989).
56.  P. GRASSBERGER and I. PROCACCIA, Phy. Rev. Lett. 50, 346 (1983).
57.  A. A. TSONIS and J. B. ELSNER, Bull. Amer. Meteorol. Soc. 70, 14
       (1989).
58.  R. POOL, Science (Washington, D. C.), 243, 1290 (1989).
59.  A. A. TSONIS, Weather, 44, 258 (1989).
60.  D. ANDREWS and P. READ, Phys. World, 2, 20 (1989).
61.  H. R. PRUPPACHER and J. D. KLETT, In Microphysics of clouds and
       precipitation. D. Reidel Publishing Co., Boston, USA, 1979, pp. 1-714.
62.  R. BOERS, J. Atmos. Sci. 28, 107 (1989).
63.  A. A. TOWNSEND, The structure of turbulent shear flow. Cambridge
       University Press, Cambridge, 1956, pp. 115-130.
64.  G. F. CHEW, Science (Washington, D. C.), 161, 762 (1968).
65.  D. BHOM, In Quantum theory, Prentice Hall, New York, 1951, pp. 1-614.
66.  I.PRIGOGINE and I. STENGERS, In Order out of chaos: man's new
       dialogue with nature. Bantam Books Inc., New York, 1984, pp.1-334.
67.  P. S. STEVENS, In Patterns in nature. Little, Brown and Co. Inc., Boston,
       USA, 1974.
68.  R. F. CURL and R. E. SMALLEY, Science (Washington, D. C.), 242, 1017
       (1988).
69.  F. STODDART, Nature (London) 334, 10 (1988).
70.  V. V. BELOSHAPKIN, A. A. CHERNIKOV, M. YA. NATENZON, B. A.
       PETROVICHEV, R. Z. SAGADEV, and G. M. ZASLAVSKY, Nature (London),
       337, 133 (1989).
71.  H. H. LAMB, In Climate: present, past and future, Vol. I. Fundamentals
       and climate now. Methuen and Co. Ltd., London, 1972, pp. 1-613.
72.  J. O. STENFLO and M. VOGEL,  Nature (London), 319, 285 (1986).
73.  R. G. HARRISON and D. J. BISWAS,  Nature (London), 321, 394 (1986).
74.  M. ALLISON,  Nature (London), 336, 312 (1988).
75.  P. T. SCHICKENDANZ and E. G. BOWEN, J. Appl. Meteorol. 16, 359
       (1977).
76.  M. LA BRECQUE, Mosaic, 18, 22 (1987).
77.  J. WARNER, J. Atmos. Sci. 27, 682 (1970).
78.  J. R.HOLTON, In An introduction to dynamic meteorology. Academic
       Press Inc., New York, 1979, pp. 1-39.
79.  R. J. DONNELLY, Sci. Am. 258, 100 (1988).
80.  V. HOGSTROM, J. Atmos. Sci. 42, 263 (1985).
81.  J. MADDOX,  Nature (London) 332, 581 (1988).
82.  A. RAE, New Sci. Nov. 27, 36 (1986).
83.  J. MADDOX,  Nature (London) 335, 9 (1988).
84.  J. MADDOX,  Nature (London) 334, 99 (1988).
85.  P. CVITANOVIC, Phys. Rev. Lett. 61, 2729 (1988).