A detailed theory of deterministic chaos is developed for atmospheric turbulence and applied to mathematically model the formation of global weather systems, climatological weather cycles and the electrical, dynamical and microphysical characteristics of clouds.
I. INTRODUCTION
Satellite cloud pictures indicate organisation of cloud patterns in rows, streets and Mesoscale (20-200 km) Cloud Clusters (MCC) as a common feature of global weather systems1 and therefore provide evidence for the existence of organised helical vortex roll circulations or large eddies in the planetary atmospheric boundary layer (ABL) extending from the earth's surface to the top of the troposphere (10-15 kms). The turbulent troposphere also sustains regular long term climatological cycles e.g., the Quasi-Biennial Oscillation (QBO) and the sunspot related 20 year cycle in weather patterns2. It is not clear how such long-lived organised circulations are maintained in the dissipative turbulent environment of the ABL3. In this paper it is shown that the universal period doubling route to chaos is the growth mechanism for organised weather systems in the global planetary atmosphere.
II. THE UNIVERSAL PERIOD DOUBLING
ROUTE TO CHAOS OR DETERMINISTIC CHAOS
Experimentally, many diverse
systems have been found to exhibit the characteristic behavior associated
with deterministic chaos, examples including chemical and biological systems
as well those from physics4. Mitchell Feigenbaum5
discovered that a few universal ratios independent of any dynamical details
characterised all systems where periods doubled as they approached turbulence.
At the point of infinite period doubling the orbits of Feigenbaum's system
showed a complex behavior in which one could discern a scale invariant
or fractal structure6. Phenomenological observation of fractal
structure in nature represents the two fundamental symmetries of nature,
namely, dilation (r®
r+c where r is the length scale and c is a constant) and
correspond respectively to change in unit of length or in the origin of
the co-ordinate system7. A self-similar object is identified
by its fractal dimension D that is defined as dlnM(R) / dlnR
where M(R) is the mass contained within a distance R from
a typical point in the object. Self-similar growth process in nature lead
to the observed universal fractal geometry of macroscopic structures in
natural phenomena. However, the basic physical mechanism of the self-organised
fractal geometry in nature is not yet identified7.
A striking example of self-similar fractal
geometry in nature is exhibited by the global cloud cover pattern. Macroscopically
different shaped clouds are self-similar fractals over a number of orders
of magnitude of length scales8. Also, the structure of the ABL
as revealed by advances in remote sensing and insitu measurement
techniques indicate scale invariant energy structure for the full continuum
of atmospheric motions which follow a power law spectrum of the form f
-n where f is the frequency and n
the exponent8. The physics of the self-similar fractal cloud
growth structures associated with deterministic chaos in the atmosphere
is not yet identified.
III. PHYSICS OF DETERMINISTIC
CHAOS IN THE PLANETARY ATMOSPHERIC BOUNDARY LAYER
Period doubling implies growth
of self-similar large eddy structures from turbulent eddies by successive
incremental length step growth equal to the turbulent eddy length. A representative
example is the organised growth of large eddy or vortex roll circulations
from the turbulence scale in the ABL and manifested as cloud rows
and streets in satellite pictures of global cloud cover9 pattern.
The Rayleigh-Benard instability observed in laboratory experiments10
simulates analogous vortex roll circulations and is an example of a self-organised
system. In summary, turbulent eddies of frictional origin at the planetary
surface posses inherent upward momentum flux which is progressively amplified
by buoyant energy supply from Microscale Fractional Condensation (MFC)
of water vapour on hygroscopic nuclei by deliquescence even in an unsaturated
environment11. Microscale Fractional Condensation (MFC)
occurs on hygroscopic nuclei when water vapour mixing ratio increases beyond
the threshold for condensation by deliquescence due to adiabatic cooling
of upward moving turbulent air parcels. The exponential decrease of atmospheric
density with height further accelerates the turbulence scale upward momentum
flux. The mean turbulence scale buoyant energy production gives rise to
the formation of progressively larger helical vortex roll circulations
in continuous succession, thereby generating a hierarchical eddy continuum.
The large eddy growth in the ABL from the turbulence scale energy
supply (energy pump) is analogous to the triggering of lower frequency
laser emission by a higher frequency laser pump in a non-linear optical
medium12. The larger eddies carry the turbulent eddies as internal
circulations which contribute to their (large eddies) further growth. A
conceptual model of the large and turbulent eddies in the ABL (
Atmospheric Boundary Layer) is given as Fig.1.
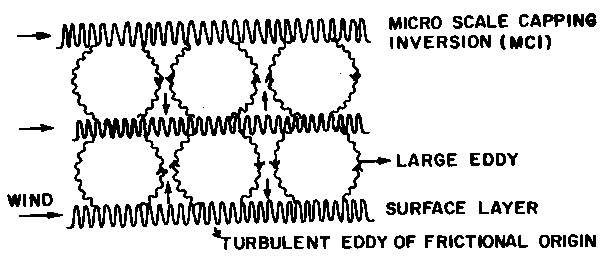
Townsend13 has investigated the structure and dynamics of large eddy formations in turbulent shear flows and has shown that large eddies of appreciable intensity form as a chance configuration of the turbulent motion as illustrated in the following example. Consider a large eddy of radius R that forms in the field of isotropic turbulence with turbulence length and velocity scales 2r and w respectively. The dominant turbulent eddy radius is therefore equal to r . The mean square circulation around a circular path of large eddy radius R is given by.
where w, w1 are the tangential velocity components at the positions of the path elements ds and ds1. If the velocity product falls to zero while the separation ds and ds1 is still small compared with the large eddy radius R, i.e., the motion in sufficiently separated parts of the flow is statistically independent
where w* is the root mean square (r.m.s) circulation speed of the small (turbulent) eddy.
The root mean square (r.m.s.) velocity of circulations
W in the large eddy of radius R is
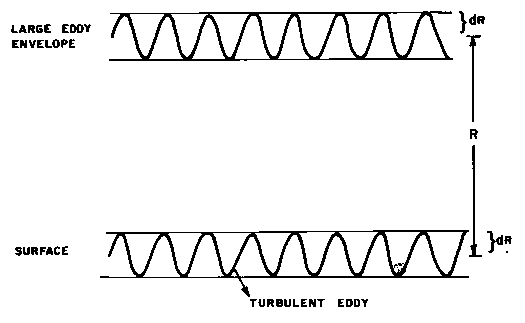
The above equation can be applied directly to derive the r.m.s. circulation speed of the large eddy of radius R generated by turbulence scale energy pump. The scale ratio z is equal to the ratio of the radii of the large and turbulent eddies. Warming and associated buoyant energy production occur by latent heat release during condensation in the environment of the turbulent eddies and therefore results in anomalous positive temperature lapse rates or Microscale Capping Inversion (MCI) layer on the large eddy envelope (Fig.1). The MCI rises up with the daytime convective growth of large eddy and may be identified with the rising inversion of the daytime ABL seen in echosonde records14. An incremental growth dR of large eddy radius equal to the turbulent eddy radius r occurs in association with an increase dW in large eddy circulation speed as a direct consequence of the buoyant velocity (w* ) production by MFC. The MCI is thus a region of wind shear and temperature inversion in the ABL. The growth of large eddies from the turbulence scale at incremental length steps equal to r (turbulence length scale doubling) is therefore identified as the universal period doubling route to chaos and MCI is therefore a region of chaos. The growth of large eddy from the turbulence scale is shown at Fig.2.
IV. DILUTION OF LARGE EDDY VOLUME BY MASS EXCHANGE WITH ENVIRONMENT
The turbulent fluctuations mix overlying environmental air into the growing large eddy volume and the non-dimensional steady state fractional volume dilution k of the total large eddy volume across unit cross section on its envelope is equal to
where w* is the unidirectional turbulent eddy acceleration and dW the corresponding acceleration of the large eddy circulation during the large eddy incremental length step growth dR equal to r.
k > 0.5 for z < 10. Therefore organised large eddy growth can occur for scale ratio z ³10 only since dilution by environmental mixing is more than half by volume and erases the signature of large eddies for scale ratio z < 10. Therefore a hierarchical, scale invariant, self-similar eddy continuum with semi-permanent dominant eddies at successive decadic scale range intervals is generated by the self-organised period doubling route to chaos growth process. The large eddy circulation speed is obtained by integrating Eq (2) for large eddy growth from the turbulence scale energy pump at the planetary surface and is given as
k = 0.4 for z = 10. This is the well-known logarithmic wind profile relationship in the ABL14 and k is designated as the Von Karman's constant and its value determined from observations is equal to about 0.415. The period doubling route to chaos growth process therefore generates a scale invariant eddy continuum where energy flow structure is in the form of nested logarithmic spiral vortex roll circulations, a complete circulation consisting of the outward and inherent compensating inward flow. The region of chaos is the dynamic growth region of large eddy by turbulence scale energy pumping and the nested vortex hierarchical continuum energy structure is manifested as the strange attractor design, a signature of organised chaos, first identified by Lorenz16 during mathematical simulation of atmospheric convection and later, widely investigated by mathematicians17. A trajectory on the strange attractor exhibits widely different paths for small differences in initial conditions thereby making long-term prediction difficult. The strange attractor design of the atmospheric continuum vortex roll circulations is manifested as the following atmospheric phenomena (1) the spiral cloud formation in hurricanes18, (2) aerosol concentration with layered fine structure observed in the stratospheric Junge aerosol layer11, the arctic haze19 and more spectacularly in the planetary rings of the major planets Jupiter, Saturn & Uranus20 and (3) the layered structure of ozone concentration in the Antarctic stratosphere21. Particles in the planetary rings may be shown to follow the relation R3 / T2 = constant from Eqs. (1) & (2) and is therefore consistent with Kepler's third law of planetary motions22.
Vertical mixing due to turbulent eddy fluctuations progressively dilutes the rising large eddy and a fraction f of surface air reaches the normalised height z given by
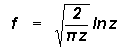
The steady state fractional air mass flux f from the surface is dependent only on the dominant turbulent eddy radius.
VI. DETERMINISTIC CHAOS AND
RICHARDSON NUMBER FOR ATMOSPHERIC TURBULENCE
The Richardson number Ri 14 that is used as an index of shear produced turbulence is defined as follows
where NB is the Brunt-Vaisala frequency14. For the atmosphere, observations show that Ri £ 0.25 in regions of turbulence in the atmosphere. In the following it is shown that Ri £ 0.25 in the Microscale Capping Inversion (MCI) for scale ratio z ³ 10 23. The Brunt-Vaisala frequency for the turbulent air parcels in the MCI is given in terms of the virtual temperature (qv) lapse rate (dqv /dR) in the MCI where an incremental growth dR per second of the large eddy is associated with a warming of dqv and an increase in wind speed dW as given below
where g is the acceleration due to gravity.
The buoyant vertical velocity w* production is a direct consequence of the temperature perturbation dq* 14
dR being the incremental large eddy growth per second is equal to dW
Ri = 1/4 for scale ratio z = 10. It was shown in an earlier section that organised growth of large eddy occurs for scale ratios z ³ 10 and in the Microscale Capping Inversion (MCI) at the crest of the large eddy the Richardson number Ri £ 0.25 and it is consistent with deterministic chaos model predictions shown above. Richardson number may therefore be alternatively considered to represent the ratio of the vertical velocity in the large eddy to that in the turbulent eddy in the region of chaos, the MCI.
In summary, the ABL consists of a semi-permanent hierarchical system of eddies consisting of the convective, meso-, synoptic and planetary scales which evolve basically from the dominant turbulence scale at successive decadic scale range intervals and is manifested as Mesoscale Cloud Clusters (MCC) and cloud rows in global synoptic weather systems. Enhanced condensation inside clouds amplifies the myriads of turbulent eddies and give rise to 'cloud top gravity oscillations' (Fig.3).
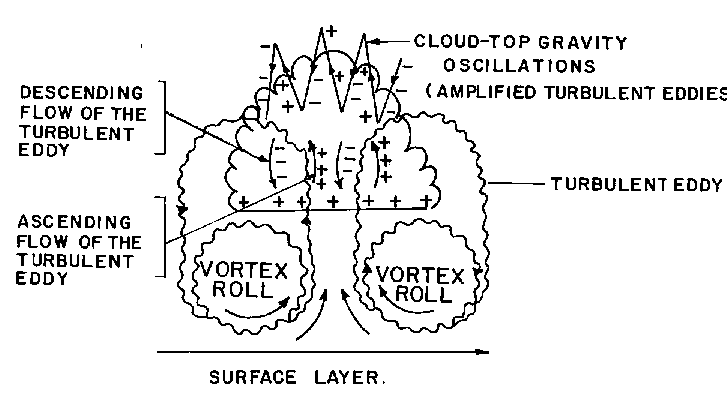
Figure 3. Cloud formation in the updraft regions of vortex roll (large eddy) circulations. The turbulent eddies get amplified in the vertical by the latent heat released by condensation of water vapour in the cloud and generate 'cloud-top gravity oscillations'. Electrical charge separation occurs inside the cloud by transport upward (downward) of positive (negative) space charges by the ascending (descending) flow of the cloud top gravity oscillations.
Cloud water condensation in the innumerable turbulent eddies is responsible for the observed cauliflower like surface granularity of the cumulus clouds. The physical mechanism of growth of the atmospheric buoyancy (gravity) waves from turbulent buoyant energy production is analogous to the Condtional Instability of the Second Kind (CISK) mechanism14 where hurricane systems are postulated to derive their energy from convective scale cloud water condensation. Also, there is an inherent two way energy feedback mechanism in the hierarchical atmospheric eddy system discussed in this paper and given by Eq (1) which is a statement of the law of conservation of energy, self-similarity and self-consistency in atmospheric processes. The full continuum of atmospheric eddies exist as a unified whole in time and space and contribute to the manifested atmospheric phenomena in the global planetary atmosphere and such a concept is similar to the 'Bootstrap' theory of Chew 24 and the theory of implicate order envisaged by Bohm25. The mechanism of evolution of the large eddies depends only on the turbulent eddy size and is therefore universal and applicable to the global planetary atmosphere and for all planetary atmospheres independent of their macroscopic size and chemical composition.
The relationship between the size (R),
time period (T), circulation velocity (W) and
energy (E) scales of the convective (c), meso- (m),
synoptic (s) and planetary (p) scale atmospheric eddy systems
to the primary turbulence scale (t) is derived from Eq (1)
and is given below26, 27.
The globally observed Quasi-Biennial Oscillation (QBO) and the 20 -year cycle in weather patterns may possibly result respectively from the fundamental semi-diurnal atmospheric pressure oscillation (QBO ~ 12 hrs x 402) and the 5 minutes oscillation of the sun's atmosphere28 (20 years ~ 5 min x 404) (Eq.5). Such a process is analogous to antistokes laser emission triggered by a laser pump12.
VI ATMOSPHERIC EDDY ENERGY SPECTRUM
The atmospheric eddy energy spectra obtained by observations of turbulence spectra of wind in the ABL show the existence of a continuous spectrum of eddies with universal characteristics of scale invariant spectral slope29,30 implying the existence of self similarity in atmospheric dynamical processes8. The universal period doubling route to chaos eddy growth mechanism is shown to be responsible for the observed scale invariant eddy energy spectrum in the atmosphere as follows:
The eddy energy power spectrum is conventionally plotted as lnE versus lnn where E is the eddy energy and n its frequency
The spectral slope S of the scale invariant eddy energy spectrum is given as
The above model prediction is consistent with observations of a universal spectral slope approaching -2 29.
VII. QUANTUM MECHANICAL NATURE
OF ATMOSPHERIC EDDY ENERGY STRUCTURE
The Kinetic energy
KE per unit mass of an eddy of frequency n
in the hierarchical eddy continuum is shown to be equal to Hn
where H is the spin angular momentum of unit mass of the
largest eddy in the hierarchy. The circulation speed of the largest eddy
in the continuum is equal to the integrated mean of all the inherent turbulent
eddy circulations. Let Wp be this mean circulation
speed or the zero level about which all the smaller frequency fluctuations
occur.
H is
equal to the product of the momentum of unit mass of planetary scale eddy
and its radius and therefore represents the spin angular momentum of unit
mass of planetary scale eddy about the eddy center. Therefore the Kinetic
energy of unit mass of any component eddy of frequency n
of the scale invariant eddy continuum is equal to
Hn
. Further, since the largest eddy is but the sum total of all the inherent
smaller scales, the large eddy energy content is equal to the sum of all
its individual component eddy energies and therefore the kinetic energy
KE distribution is normal and the kinetic energy KE of any
eddy of radius R in the eddy continuum expressed as a fraction
of the energy content of the largest eddy in the hierarchy will represent
the cumulative normal probability density distribution. The eddy continuum
energy spectrum is therefore the same as the cumulative normal probability
density distribution plotted on a log-log scale, i.e., the eddy
energy probability density distribution is equal to the square of the eddy
amplitude. Therefore the eddy continuum energy structure follows quantum
mechanical laws31. The energy manifestation of radiation and
other subatomic phenomena appear to possess the dual nature of wave and
particles since one complete eddy energy circulation structure is inherently
bi-directional and associated with corresponding bimodal form of manifested
phenomena, e.g., formation of clouds in the updraft regions and dissipation
of clouds in the downdraft regions giving rise to discrete cellular structure
to cloud geometry. Also from Eq. (7)
The above statement is analogous to Heisenberg's uncertainty principle for subatomic dynamics31. In the context of the atmospheric eddy continuum the above equation implies that large changes in eddy energy can occur only during short intervals of time and vice-versa, illustrative examples being the hurricane systems on the one hand and climate changes on the other.
VIII. STATISTICAL DISTRIBUTION
CHARACTERISTICS OF THE ATMOSPHERIC EDDY CONTINUUM
Fundamental classical statistical
distribution functions commonly occurring in natural phenomena are shown
in the following to be inherent characteristics of the universal period
doubling growth phenomena. The distribution of means for sample size n
has a variance W22 that is related
to the population variance W12
as follows32.
The above statistical relation may be
derived from Eq.(1) in the context of the variance of the eddy parameters
for two different ratios z1 and z2
where n = z2 / z1 as follows
For eddy growth from smaller scale to the larger scale the ratio of eddy energy for unit mass of large eddy to that of turbulent eddy is equal to 1/n where n is the scale ratio. The eddy continuum generated by the successive integration of smaller scale circulations into large-scale circulation patterns will therefore have eddy energy spectral slope S given as
S = - 2 is in agreement with earlier derivation (Eq.6) for large-scale ratios. Since large eddy energy is the integrated mean of all inherent small scale eddies, in general, coarse mesh observations give a spectral slope - 2 for the eddy energy spectrum, e.g., climatological data23.
IX PHYSICAL MEANING OF NORMAL DISTRIBUTION PARAMETERS
In the following it is shown that the
universal period doubling route to chaos growth phenomena in the atmosphere
gives rise to the observed statistical normal distribution characteristics
for atmospheric phenomena as a natural consequence. The period doubling
growth is initiated and sustained by the turbulent (fine scale) eddy acceleration
w*
across unit cross section that then propagates by the inherent property
of inertia of the medium.
In the context of atmospheric turbulence, the statistical parameters, mean, variance, skewness and kurtosis represent respectively the net vertical velocity, intensity of turbulence, vertical momentum flux and intermittency of turbulence and are given respectively by w* , w*2, w*3, w*4 . The momentum coefficient of skewness equal to zero and the moment coefficient of kurtosis equal to 3 are the characteristics of the normal distribution32 . In the following it is shown that the observed normal distribution characteristics of atmospheric phenomena is a signature of deterministic chaos.
By analogy, the perturbation speed w* (motion) per second of the medium sustained by its inertia represents the mass, w*2 the acceleration or force, w*3 the momentum (or potential energy) and w*4 the spin angular momentum since an eddy motion has an inherent curvature to its trajectory. The eddy motion is inherently symmetric with bi-directional energy flow and therefore the skewness factor w*3 is equal to zero for one complete eddy circulation thereby satisfying the law of conservation of momentum. The moment coefficient of kurtosis is given by (dw) 4 / w*4 and represents the relative magnitude of the spin angular momentum of large eddy generated by the period doubling growth from the turbulent eddy. The statistical moment coefficient of kurtosis (dW)4/ w*4 represents the intermittency of turbulence and is shown in the following to be equal to 3 as a natural consequence of the growth phenomenon by the period doubling route to chaos.
Organised eddy growth occurs for scale ratio equal to 10 and identifies the large eddy on whose envelope period doubling growth process occurs. Therefore for a dominant eddy
(dz/z) = 1/2 for one length step growth by period doubling process since z = dz + dz .
In other words, period doubling growth phenomena result in a threefold, increase in the spin angular momentum of the large eddy for each period doubling sequence. This result is consistent since period doubling at constant pump frequency involves eddy length step growth dR an either side of the turbulent eddy length dR . The intermittency of turbulence i.e. episodes of turbulent fluctuations on relative time scale is also equal to 3.
X. PHYSICS OF THE GENERALISED
SCALE INVARIANCE FOR THE ATMOSPHERIC EDDY CONTINUUM ENERGY SPECTRA
The scale invariant atmospheric eddy continuum of the form f- -n, where f is the frequency and n the exponent observed in the ABL30 is shown to be the result of eddy growth by the universal period doubling route to chaos, the exponent n being a function of the scale ratio.
The eddy energy spectrum is shown (see Section VII) to be the same as the cumulative normal probability curve plotted on a log-log scale. The eddy energy spectral slope is derived from the cumulative normal probability distribution curve as follows. The period doubling sequence generates a large eddy of radius R equal to 2r, so that the cumulative probability of occurrence P1 of turbulent eddy fluctuations of either sign is given by (0.5r /(R+r)) and is equal to .167 (=1/6) in close agreement with the cumulative normal probability value corresponding to one standard deviation s . The cumulative normal probabilities and corresponding slopes on log-log scale for standard deviation 1s , 2s and 3s are given in Table 1. The slope of the log-log plot of cumulative normal probability distribution curve at one standard deviation is equal to -1.8 in agreement with computed (see Section VIII) and observed33 values and relates to coarse mesh observations e.g., climatological data.
The eddy energy spectral slope becomes steeper than -2 with high resolution (fine scale) observations30 which include perturbations due to more than one period doubling sequence as shown below.
Considering period doubling of large eddy R giving rise to larger eddy of length R2 = 2R considerations as above give a cumulative probability of occurrence P2 of large eddy length R equal to (0.5R / (R+R2)) = 1/6 » 0.167. Therefore the cumulative probability of occurrence of turbulent length scale r in the large eddy length section R2 is equal to P1 x P2 = 1/36 = 0.028 in close agreement with cumulative normal probability value corresponding to two standard deviation (2s .) (Table 1). The slope of the eddy energy spectrum as derived from the log-log plot of the cumulative normal probability curve is -5 at 2s (Table 1). Steep spectral slopes for localised eddy energy spectra are associated with regions of energy concentration such as severe weather systems. Eddy energy spectral slopes steeper, than -2 have been reported in the ABL30. Similarly period doubling associated with R2 corresponds to cumulative probability of occurrence equal to (1/36)» 0.0008 of the primary turbulence scale eddy at three standard deviations and the corresponding eddy energy spectral slope is -10 (Table 1).
In summary, period doubling at one standard deviation generates a semi-permanent dominant large eddy with scale ratio equal to 10 with respect to the fine scale turbulent eddy and a corresponding eddy energy spectral slope equal to -1.8. It may also be inferred that the primary period doubling in successive cumulative radial length steps r, 2r, 3r ,etc.,generated perturbations of increasing magnitude w*sinq for q = 0 to 90o so that the eddy energy spectrum has positive slope for the primary eddy circulation updraft half cycle. At the completion of one complete primary eddy circulation the spectral slope becomes equal to zero and with the generation of large eddies by space-time integration of complete cycles of small-scale fluctuations, the spectral slope becomes negative.
The scale ratio for the period doubling at one standard deviation is equal to 10 with respect to the turbulence scale. If the turbulence scale itself is assumed to consist of 10 successive sections, then the primary scale ratio at one standard deviation is equal to 100 and by similar reasoning the scale ratios at 2s and 3s are respectively equal to 1002 and 1004.
XI PHYSICAL MEANING OF
THE UNIVERSAL FEIGENBAUM'S CONSTANTS OF THE PERIOD DOUBLING ROUTE TO CHAOS
The universal period doubling route to chaos has been studied extensively by mathematicians. The basic example with the potential to display the main features of the erratic behaviour is the Julia model17 given below.
The above non-linear model represents the population values of the parameter X at different time periods n, and L parameterises the rate of growth of X for small X.
The Eq.(1) representing large eddy growth
as integrated space time mean of turbulent eddy fluctuation given as ![]() is analogous to the Julia model since large eddy growth is dependent
on the energy input from the turbulence scale with ordered two way energy
feedback between the larger and the smaller scales. Therefore the well-established
abstract mathematical results for the Julia model can be interpreted
in terms of physical processes occurring in nature as follows. Feigenbaum's5
research showed that the following two universal constants a
and d are independent of the details of the non-linear equation
for the period doubling sequence:
is analogous to the Julia model since large eddy growth is dependent
on the energy input from the turbulence scale with ordered two way energy
feedback between the larger and the smaller scales. Therefore the well-established
abstract mathematical results for the Julia model can be interpreted
in terms of physical processes occurring in nature as follows. Feigenbaum's5
research showed that the following two universal constants a
and d are independent of the details of the non-linear equation
for the period doubling sequence:
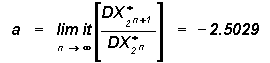
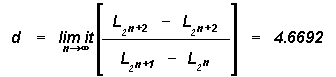
a and d therefore denote the successive spacing ratios of X* and L respectively for adjoining period doublings.
The universal constants a and d assume different numerical values for period tripling, quadrupling etc., and the appropriate values are computed by Delbourgo17 and shown to follow the relation 3d = 2a 2 over a wide domain.
The physical concept of large eddy growth by the period doubling process enables to derive the universal constants a and d and their mutual relationship as functions inherent to the scale invariant eddy energy structure as follows.
From Eq. (1) the function a may be defined as
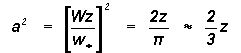 (8)
(8)
a is therefore equal to 1/k from Eq.(2) where k is the Von Karman's constant representing the non dimensional steady state fractional volume dilution rate of large eddy by turbulent eddy fluctuations across unit cross section on the large eddy envelope. Therefore a represents the non-dimensional total fractional mass disperson rate and is inherently negative. The variable a2 represents the fractional energy flux into the large eddy environment. Let d represent the ratio of the spin angular moments for the total mass of the large and turbulent eddies
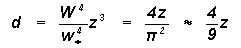 (9)
(9)
Therefore 2a2 = 3d
from Eqs.(8) & (9). The variable 2a2 represents
the total eddy energy flux into the medium. The spin angular momentum of
the resulting large eddy accounts for the observed value of three for the
moment coefficient of kurtosis of the normal distribution (see Section
IX). Therefore the above equation relating the universal Feigenbaum's
constants is a statement of the law of conservation of energy, i.e. the
period doubling growth process generates a threefold increase in the spin
angular momentum of the resulting large eddy and propagates outward as
the total large eddy energy flux in the medium. The property of inertia
enables propagation of turbulence scale perturbation in the medium by release
of the latent energy potential of the medium. An illustrative example is
the buoyant energy generation by water vapour condensation in the updraft
regions in the atmospheric boundary layer.
The universal Feigenbaum's constants a and d are respectively to -2.52 and 4.05 as computed from Eqs.(8) & (9) since the scale ratio z is equal to 10 for the self organised eddy growth mechanism in the atmospheric boundary layer.
XII. DETERMINISTIC CHAOS AND ORGANISED WEATHER SYSTEMS IN THE ABL
The global weather systems are the patterns of eddy energy manifestation in time and space of the rhythm of the unified whole of the planetary atmospheric eddy continuum. There is inherent coupling and continuity of global weather systems in time and space with universal characteristics for the thermodynamic anomaly patterns with respect to the normalised length scale. In the following, the model predicted9 unique thermodynamic anomaly patterns for the most intense weather system, the hurricane is compared with precise well-established observational results.
It was shown earlier (Section IV) that the wind profile in the ABL follows the logarithmic law. Since large eddy growth involves increase in radius simultaneous with angular displacement from origin, the trajectory of airflow associated with the large eddies will follow a logarithmic spiral pattern both in the horizontal and vertical. The complete eddy circulation consisting of the ascent and the return descent airflow therefore occurs in the form of logarithmic spiral vortices34. The full continuum of atmospheric eddies exist as a unified whole in the form of vortices within vortices as displayed in the extreme cases of the tornado funnel and the dust devil.
Spiral cloud bands of cyclone systems
The spiral airflow track for a synoptic scale large eddy is shown at Fig.4.
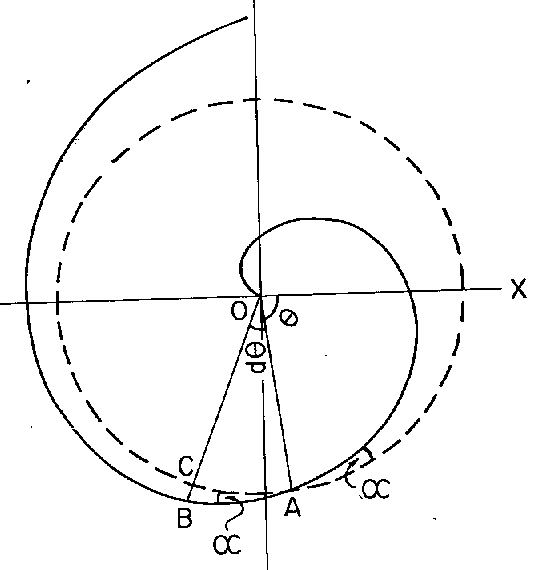
The eddy growth originating from O follows the spiral curve OAB. The angular rotation from the origin at location A is measured with respect to the axis OX.
Let OA and OB denote the
locations of the large eddy radii* R and ![]() for a growth period of one second.
for a growth period of one second.
AB will also represent the tangent to the spiral at A for a limited range. The angle BAC between the logarithmic spiral and its tangent is called the crossing angle a of the spiral.
Substituting b = tan a ; and integrating for eddy growth from r to R the above equation gives
This is the equation for an equiangular logarithmic spiral when the crossing angle is a constant.
At any location A the horizontal airflow path into a synoptic scale cyclone system follows a logarithmic spiral track.
Storm intensity and cloud band configuration
The cloud bands identify the circulation
path of the synoptic cyclonic eddy whose radial growth dR
is equal to the dominant turbulent eddy radius r and dq
is the corresponding angular rotation.
The dominant turbulent eddy radius determines the angular turning dq and incremental large eddy radius growth dR and therefore the synoptic scale spiral cloud band has different crossing angles and band widths at different locations with respect to the storm center. Observations show that increased condensation results in decrease in dominant turbulent eddy radius23. There is heavy condensation close to the storm center in association with tighter coiling of the spiral with overlapping cloud bands.
Dvorak35 has classified cyclonic storms according to the appearance of cloud bands as related to observed storm intensities. The cloud band pattern relating to the categories T1(a) to T4(a) of the Dvorak classification are simulated by suitably altering r along the radial distance R and computing R and cloud band width from equations given above. The model simulated cloud bands and the corresponding Dvorak cloud diagrams are given in Fig.5 and there is good agreement between the two.

Growth time of the eddy system
The eddy growth time T
for an eddy radius R is computed as follows.
where li is the logarithm integral or the Soldner's integral.
Horizontal profile of cyclone pressure field
The low-pressure field of the cyclone
system is created by the upward ascent of surface air. At any location
distance R from the storm center O there is an upward
mass flux of air equal to w*r
per second across unit area where r
is the air density and w*
is the production of vertical velocity per second by MFC at surface
layers. A synoptic scale weather system which has been in existence for
a time period TN and extending to a radial distance
RN developes a central pressure departure equal
to w*rTN
with respect to the ambient pressure field at the periphery X. At
the intermediate location B the corresponding pressure departure
is equal to w*rTR
where TR is the time period for the eddy to grow
from B to X. The normalised pressure departure NPD
at the intermediate location with respect to the extreme pressure departure
at the storm center is computed as
The horizontal profile of the hurricane pressure field normalised to the ambient pressure given by NPD in the above equation is computed for the 6 categories T1(a) to T6(a) of the Dvorak storm intensity categories and shown at Fig.6.

The computed horizontal profile of NPD closely resembles the corresponding log / linear pressure profiles for the nine Florida hurricanes by Holland36.
Horizontal profile of wind
The horizontal profile of wind in a cyclone system follows the logarithmic law and depends only on the turbulent eddy radius. The horizontal wind profile for the 6 categories of storm intensities T1(a) to T6(a) of the Dvorak35 classification are computed and shown at Fig.7.
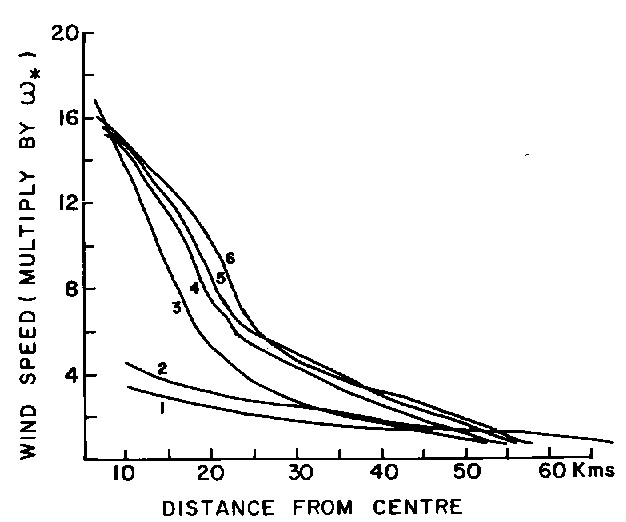
The model predicted wind variation with distance from storm center resembles the observed wind field around storms reported by several workers18,36,37.
The airflow speed is due mainly to the dynamic buoyant energy production by MFC and thus is not influenced by the rotation of the earth. Therefore the Coriolis force does not influence the airflow into the synoptic scale eddy in agreement with theoretical studies by other workers38.
XII. DETERMINISTIC CHAOS AND CLOUD PHYISCAL PROCESSES
![]() Cloud
growth occurs in the updraft regions of vortex roll circulations in the
low-pressure field of synoptic scale systems. From the theory of atmospheric
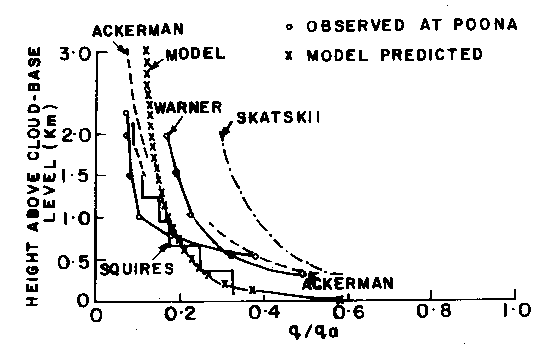
eddy dynamics it is derived and shown39 (i) the vertical profile
of the ratio of the actual cloud liquid water content (q)
to the adiabatic liquid water content (qa
) follows the f distribution (Fig.8)
Cloud
growth occurs in the updraft regions of vortex roll circulations in the
low-pressure field of synoptic scale systems. From the theory of atmospheric
eddy dynamics it is derived and shown39 (i) the vertical profile
of the ratio of the actual cloud liquid water content (q)
to the adiabatic liquid water content (qa
) follows the f distribution (Fig.8)
(2) the vertical profiles of the vertical velocity W and the total cloud liquid water content qt are respectively given by W = w* f z and qt = q* f z where t represents the total values and * represents cloud base values (3) the cloud growth time where li is the logarithm integral (4) the cloud drop size spectrum follows the naturally occurring Junge aerosol size spectrum11 and (5) the computed raindrop size spectrum closely resembles the observed Marshall-Palmer raindrop size distribution20 at the surface.
XIV DETERMINISTIC CHAOS AND ATMOSPHERIC ELECTRIFICATION
Fair Weather Electric Field and Geomagnetic Field
The atmospheric eddy continuum circulations give rise to vertical mass exchange in the ABL such that a net positive space charge current flows upward with a simultaneous downward transport of negative space charges from ionospheric levels and this dynamical two way charge transport is shown to be of the right order of magnitude and direction to sustain the fair weather atmospheric electric field and also explain the horizontal component of the geomagnetic field distribution41. The above theory also helps to explain the observed42 close similarity between the geomagnetic field lines and atmospheric circulation patterns. Therefore changes in atmospheric circulation patterns preceding climatic changes can be detected in geomagnetic field pattern variations. The wandering of the geomagnetic North Pole is therefore closely related to global climatic variation and incidentally also is reflected in the subatomic dynamics of ferromagnetic substances, which naturally align themselves along geomagnetic N-S direction.
Cloud Electrification
It is shown that cloud top gravity oscillations mix overlying environmental air into the cloud such that there is a downward transport of negative space charges from above cloud top regions and a simultaneous upward transport of positive space charges from below cloud base levels to the cloud top region (Fig.3). Positive dipole cloud charging occurs by the vertical mixing. The electric field at the surface due to the cloud dipole charge, the strength of the cloud dipole, the cloud electrical conductivity, the point discharge current are expressed in terms of the basic non-dimensional parameters f and z43.
XV DETERMINISTIC CHAOS AND ATMOSPHERIC URBAN EFFECTS
The thermal energy input from industrial / urban sites in combination with hygroscopic nuclei and moisture lead to enhanced cloud growth process with taller clouds and heavier rainfalls particularly in the downwind region. A fraction f of the surface nuclei form cloud / raindrops and therefore the same fraction f of atmospheric pollution content will also get washed down in the rain. Even in clear weather conditions the pollution content of atmospheric air in the form of aerosols will be equal to a fraction f of the value at the source location. The steady state flux of pollution transport is therefore given by the f distribution both in the horizontal and vertical. Though f is small at large values of the normalised distance z, yet long term accumulation of pollution will be appreciable resulting in irreversible environmental degradation. Also enhanced dynamics associated with thermal energy supply from urban industrial sites leads to a faster transport of pollutants in all directions.
XVI DETERMINISTIC CHAOS AND STRATOSPHERIC DYNAMICS
Thermal energy sources are regions of enhanced eddy dynamics and vertical mixing extending to the stratosphere and above. Enhanced downward flux of stratospheric ozone occurs above regions of industrial / urban activity. Beig and Chakravorthy44 have reported a sharp decrease in stratospheric ozone in association with a major fire in an offshore oil well in India. Downward transport of stratospheric ozone occurs in regions of deep convection45. Stratospheric aerosol and radioactive debris from volcanic eruptions and nuclear experiments / accidents are transported downwards to surface levels in regions of deep convection where intense vertical mixing occurs. Such regions of stratospheric contamination deposition on surface, even in fair weather will occur in discrete areas of fractal nature analogous to rainfall areas8 and thus may account for the radiation hot spot fall out pattern reported following the Chernobyl nuclear reactor accident46. Also, the recently reported ozone hole in the Antarctic stratosphere may possibly be caused by enhanced vertical mass exchange due to increased international exploration activities in Antarctica during the spring / summer season in recent years.
XVII DETERMINISTIC CHAOS AND IONOSPHERIC DYNAMICS
It is known that solar flares perturb the ionosphere and cause intensification of weather systems47. Therefore ionospheric heating experiments and the numerous earth orbiting satellites may possibly create fine scale magnetosphere / ionospheric perturbations and lead to inadvertent modification of climate.
XVIII CONCLUSIONS
Deterministic chaos in the planetary atmospheric boundary layer is identified as the growth of large eddy (helical vortex roll circulation) from turbulence scale buoyant energy generation with implicit ordered two way energy feed back mechanism between the larger and smaller scales. It is shown that such a process generates a scale invariant, hierarchical self-similar atmospheric eddy continuum energy structure with dominant eddies (limit cycles) at decadic scale range intervals as manifested in Meso-scale Cloud Clusters (MCC) and the fractal geometry of cloud cover pattern. Further, the eddy continuum energy structure obeys quantum mechanical laws and the apparent wave-particle duality is attributed to the inherent bi-directional eddy energy flow associated with bimodal phenomenological manifestation e.g., formation of clouds in updrafts and dissipation of clouds in downdrafts of the eddy circulation. The pressure and wind anomaly patterns of global weather systems and the cloud electrical, microphysical and dynamical characteristics could result from the simple universal unique functions of the turbulence scale energy generation. The universal Feigenbaum's constants a and d defining the period doubling growth process in the atmosphere are respectively equal to -2.52 and 4.05 in agreement with mathematical computations. The universal relation 2a2=3d is shown to be a statement of the law of conservation of energy for the period doubling growth process, since period doubling growth on either side of the primary turbulent eddy generates a threefold increase in the spin angular momentum (3d) of the resulting large eddy and is equal to the total energy flux (2a2) into the environment of the large eddy.
The bi-directional energy flow in the planetary atmospheric eddy continuum is manifested as various tropospheric, ionospheric and magnetospheric phenomena in a continuous chain of individual perturbation events in a space-time continuum which is super symmetric in the macroscale ABL, being the fusion of the individual component eddy, symmetries.
ACKNOWLEDGEMENTS
The authors expresse their deep gratitude to Dr. A. S. R. Murty for his keen interest and encouragement during the course of this study.
1. L. Eymard, J. Atmos. Sci., 42, 2844 (1985).
2. W. Burroughs, New Scientist, 10 July, 36 (1986).
3. H. Tennekes, In: Workshop on Micrometeorology (Amer. Meteorol. Soc., Boston, USA, 1973).
4. W. Fairbairn, Phys. Bull., 37, 300 (1986).
5. M.J. Feigenbaum, Los Alamos Sci., 1, 4 (1980).
6. B.J. Levi, Physics Today, April, 17 (1986).
7. L.P. Kadanoff, Physics Today, Feb., 6 (1986).
8. S. Lovejoy and D. Schertzer, Bull. Amer. Meteorol. Soc., 67, 21 (1986).
9. A. Mary Selvam, Proc. Int'l Conf. Monsoon and Mesoscale Meteorology, Nov. 4-7, Taipei, Taiwan, 84 (1986).
10. G. Ananthakrishna, Bull. Sci., Jul.-Aug., 20 (1986).
11. H.R. Pruppacher and J.D. Klett, Microphysics of clouds and precipitation (D. Reidel Publishing Co., Boston, USA, 1978).
12. R.G. Harrison and D.J. Biswas, Nature, 321, 394 (1986).
13. A.A. Townsend, The structure of turbulent shear flow (Cambridge University Press, Cambridge, 1956).
14. J.R. Holton, An introduction to dynamic meteorology (Academic Press, New York, 1979).
15. U. Hogstrom, J. Atmos. Sci., 42, 263 (1986).
16. E.N. Lorenz, J. Atmos. Sci., 30, 130 (1963).
17. R. Delbourgo, Asia-Pacific Physics News, 1, 7 (1986).
18. R.H. Simpson and H. Riehl, The hurricane and its impact (Lousiana State University Press, London, 1981).
19. L.F. Radke, J.H. Lyons, I.H. Bailey and P.V. Hobbs, Preprints, 11th Int'l Conf. Atmospheric Aerosols, Condensation and Ice Nuclei, Sept. 3-8, Budapest, Hungary, Vol.I, 138 (1984).
20. F.C. Michel, Geophys. Res. Letts., 13, 442 (1986).
21. D.J. Hofmann, J.W. Hardes, S.R. Rolf and J.M. Rosen, Nature, 326, 59 (1987).
22. B. Yavorsky and A. Detlaf, Handbook of Physics (Mir Publishers, Moscow, 1975).
23. A. Mary Selvam, A.S. Ramachandra Murty and Bh.V. Ramana Murty, Proc., IX Int'l Cloud Physics. Conf. Aug., 21-28, Tallinn, USSR, 387 (1984).
24. G.F. Chew, Science, 161, 762 (1968).
25. D. Bohm, Quantum Theory (Prentice Hall, New York, 1951).
26. A. Mary Selvam and A.S.R. Murty, Proc., Int'l Conf. Energy Transformations and Interactions with Small and Mesoscale Atmospheric Processes, March 2-6, Switzerland (1987).
27. A. Mary Selvam, Proc., 5th Conf. Applied Climatology, Amer. Meteorol., Soc., March 9-13, Baltimore, Mary Land, USA (1987).
28. J.O. Stenflo and M.O. Vogel, Nature, 319, 285 (1986).
29. T.E. Van Zandt, Geophys. Res. Letts., 9, 575 (1982).
30. K.S. Gage, B.B. Balsley and R. Garello, Geophys. Res. Letts., 13, 1125 (1986).
31. R.P. Feynman, R.B. Leighton and M. Sands, The Feynman lectures on physics (Addison-Wesley Publishing Co., Inc., London, 1964).
32. M.R. Speigel, Theory and problems of Statistics (Shaum's outline series, McGraw-Hill Book Company, N.Y., 1961).
33. S. Lovejoy and D.Schertzer, Ann. Geophysicae (1985).
34. T. Hauf, Centr. Atmos. Phys., 58, 380 (1985).
35. V.P. Dvorak, Mon. Wea. Rev., 103, 420 (1975).
36. G.J. Holland, Mon. Wea. Rev., 108, 1212 (1980).
37. G.R. Atkinson and C.R. Holliday, Mon. Wea. Rev., 105, 241 (1977).
38. J.W. Diercks and R.A. Anthes, J. Atmos. Sci., 33, 959 (1976).
39. A. Mary Selvam and A.S.R. Murty, Proc. 4th WMO Scientific Conf. Wea. Mod., Aug. 12-14 Honolulu, Hawaii, 503 (985).
40. R.R. Rogers, A short course in cloud physics (Pergamon Press, N.Y., 1976).
41. A. Mary Selvam, Proc. Int'l Geoscience and Remote Sensing Symposium '87 (IGARSS '87), May 18-21, University of Michigan, USA (1987).
42. J. Gribbins, New Scientist Feb. 5, 350 (1981).
43. A. Mary Selvam, A.S.R. Murty, G.K. Manohar, S.S. Kandalgaonkar and Bh.V. Ramana Murty, Proc., VIIth Int'l Conf. Atmos. Elec., June 3-8, Albany, N.Y., USA, (1984).
44. E. Beig and D.K. Chakravorty, New Scientist, July 31, 25 (1986).
45. G.P. Gushchin and S.A. Sokolenko, Soviet Meteor. and Hydrology, 10, 36 (1985).
46. Nature, News, Chernobyl accident, Nature, 322, 765 (1986).
47. J.R. Herman and R.A. Goldberg, Sun, Weather and Climate (NASA Report SP-426, Washington D.C., USA, 1978).
| Deviation
(s = standard deviation) |
Cumulative
occurrence frequency |
Slope of cumulative
occurrence frequency curve (log-log scale) |
|
|
|
|
|
|
|
|
|
|
|
|
Figure 1. Conceptual model of large and turbulent eddies in the ABL
Figure 2. Growth of large eddy from the turbulent eddies originating at the planetary surface.
Figure 3. Cloud formation in the updraft regions of vortex roll (large eddy) circulations. The turbulent eddies get amplified in the vertical by the latent heat released by condensation of water vapour in the cloud and generate 'cloud-top gravity oscillations'. Electrical charge separation occurs inside the cloud by transport upward (downward) of positive (negative) space charges by the ascending (descending) flow of the cloud top gravity oscillations.
Figure 4. The spiral air flow track in hurricanes.
Figure 5. Deterministic chaos model prediction of the hurricane spiral cloud bands (second row) and Dvorak cloud diagrams (first row) for storm intensities T1(a) to T4(a) .
Figure 6. Deterministic chaos model prediction of horizontal surface pressure field pattern for hurricanes.
Figure 7. Deterministic chaos model prediction of the horizontal wind field pattern for hurricanes.
Figure 8. Deterministic chaos model prediction of the vertical profile of the ratio of cloud liquid water content (q) to the adiabatic liquid water content (qa) and comparison with observations (J. Warner, J. Atmos. Sci., 27, 682-688, 1970)