2.5 Fivefold and Spiral Symmetry Associated with Fibonacci Sequence
The ratio of adjacent elements of the Fibonacci sequence approaches the irrational number t =(1+Ö 5)/2 in the limit. The number, t is the solution to the algebraic equation
1 + x = x2
As a result t has the property
1+ t = t 2
Therefore, the double geometric sequence
![]()
![]()
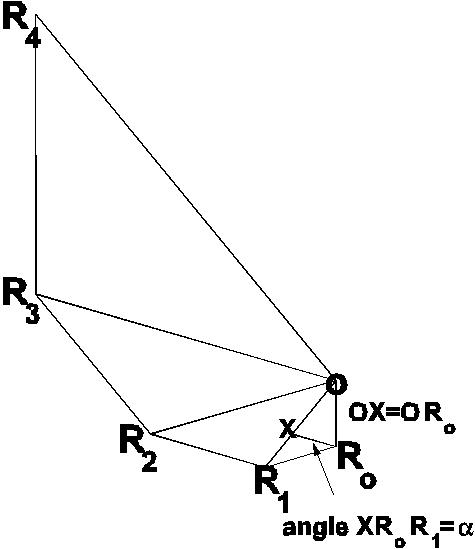
![]() is the Fibonacci sequence since it has the property that each term is equal to the sum of the earlier two terms and also the ratio of each term to the earlier term is equal to the golden mean t . It is the only geometric series which is also a Fibonacci sequence (Kappraff, 1992 References). The Fibonacci numbers can be represented geometrically in polar coordinates in two dimensions by the equiangular spiral RoR1R2R3R4R5... drawn with origin O, with lengths of successive radii OR0, OR1, OR2, ......... and corresponding spiral segments RoR1, R1R2, R2R3, ...... following Fibonacci mathematical sequence (Figure 5).
is the Fibonacci sequence since it has the property that each term is equal to the sum of the earlier two terms and also the ratio of each term to the earlier term is equal to the golden mean t . It is the only geometric series which is also a Fibonacci sequence (Kappraff, 1992 References). The Fibonacci numbers can be represented geometrically in polar coordinates in two dimensions by the equiangular spiral RoR1R2R3R4R5... drawn with origin O, with lengths of successive radii OR0, OR1, OR2, ......... and corresponding spiral segments RoR1, R1R2, R2R3, ...... following Fibonacci mathematical sequence (Figure 5).
RoR1 may be considered to be the tangent at Ro to the circle with center O and radius ORo. The angle R1RoX equal to angle a which the tangent makes with the arc XRo is the crossing angle of the spiral RoR1R2...
The initial radius ORo equal to R grows to OR1 equal to R + dR after an angular turning RoOR1 equal to dq . The incremental growth dR is equal to the length R1X in Figure 5.
FIGURE 5
Therefore
tan (a )=R1X/ARo
XRo = Rdq for the arc XR0 of circle with center O and radius OR0 equal to R.
tan (a ) = a in the limit for small values of a .
Therefore
![]()
or
![]()
Integrating for growth of radius from r to R associated with angular turning from 0 to q
![]()
or
![]()
Geometrical consideration for generation of the Fibonacci spiral in three dimensions specify a constant angular turning dq equal to 1/t between successive radii and therefore a constant crossing angle, also equal to 1/t The Fibonacci equiangular spiral is then given by the relation
![]()
The angle subtended at the center between two successive radii is therefore equal to the golden angle
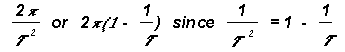
The Fibonacci equiangular spiral as shown in Figure 6 has intrinsic internal structure of the quasiperiodic Penrose tiling pattern (see Section 2.6) and associated long-range spatial and temporal correlations.
FIGURE 6
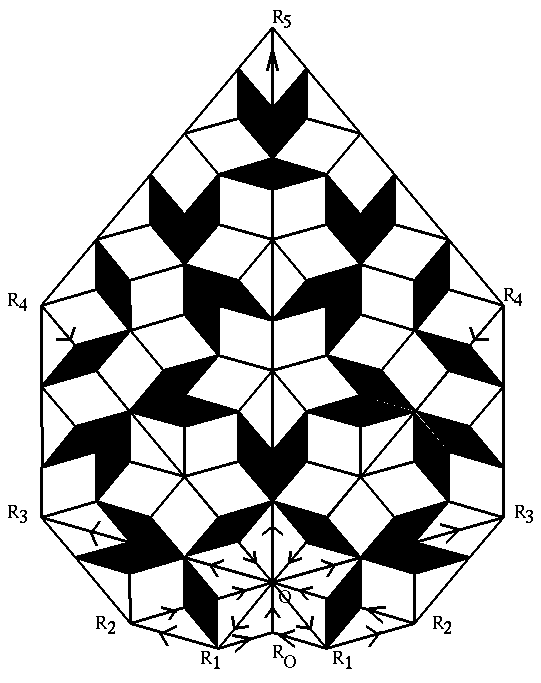
The Fibonacci spiral is traced with mathematical precision in nature in the dynamical growth processes of plants as seen in the geometrical placement on the shoot, of primordia, which later develop into the various plant parts. In a majority (92%) of plants studied world wide, successive primordia always subtend angle equal to the golden angle at the apical center (Jean, 1994 References). Primordia placement in space and time may therefore be resolved into the precise geometrical pattern of the quasiperiodic Penrose tiling pattern.