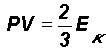
Cantorian Fractal Space-Time Fluctuations in Turbulent Fluid Flows and the Kinetic Theory of Gases

A.M.Selvam

Indian Institute of Tropical Meteorology, Pune 411 008, India

(Retired email: selvam@ip.eth.net)

Web site: http://www.geocities.com/CapeCanaveral/Lab/5833
 
 

Abstract

Fluid flows such as gases or liquids exhibit space-time fluctuations on all scales extending down to molecular scales. Such broadband continuum fluctuations characterise all dynamical systems in nature and are identified as selfsimilar fractals in the newly emerging multidisciplinary science of nonlinear dynamics and chaos. A cell dynamical system model has been developed by the author to quantify the fractal space-time fluctuations of atmospheric flows. The earth's atmosphere consists of a mixture of gases and obeys the gas laws as formulated in the kinetic theory of gases developed on probabilistic assumptions in 1859 by the physicist James Clerk Maxwell. An alternative theory using the concept of fractals and chaos is applied in this paper to derive these fundamental gas laws.

1.   Introduction

The kinetic theory of gases is based on the statistical method of investigation (Yavorsky and Detlaf, 1975; Ruhla and Barton, 1992).

The basic gas law for a perfect gas is

(1)
where P = pressure of the gas and

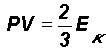
V = volume of the gas

and

(2)
where Ekis the total kinetic energy of translatory motion of n molecules of the gas occupying the volume V. Using classical mechanics, i.e. Newton's second law of motion, the pressure P exerted by the molecules in a closed box of volume V is derived as

(3)
where

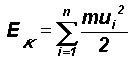
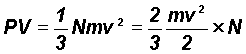
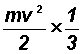
represents the average kinetic energy of a molecule of mass m in any direction, i.e. the average for the three Cartesian co-ordinates x, y, z.

The distribution of molecular speeds was derived by Maxwell based on three probabilistic assumptions, namely (i) uniform distribution in space, (ii) mutual independence of the three velocity components and (iii) isotropy as regards the directions of the velocities (Ruhla and Barton, 1992). These assumptions were also used in deriving the fundamental gas law at Eq.(1) for a perfect gas. Maxwell's distribution of molecular speeds is given by the following equation.


(4)
where r(v) is the probability density assigned to the speed v , T is the absolute temperature of the perfect gas, m is the mass of a molecule and k is the Boltzmann's constant .

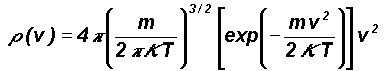
For a given gas at a fixed temperature T , the probability density r(v) may be written as

r (v) µ exp(-v2 ) v2

(5)
A graph of Maxwell's distribution of molecular speeds is shown in Fig.1 below.


 
 
 
 

2. Cell dynamical system model for kinetic theory of gases

The above equations for the kinetic theory of gases can be derived directly from the cell dynamical system model (Selvam et al., 1984a,b ; 1992; 1996; Sikka et al., 1984; Selvam and Murty, 1985; Selvam, 1988; 1989; 1990;1993; 1997; 1998; 1999; 2000; Selvam and Joshi, 1995; Fadnavis and Selvam, 1997; Selvam and Fadnavis, 1998; 1999a,b,cReferences) as follows. The random thermal agitation (fluctuation) of molecular speeds is analogous to a continuum of eddy circulations, that is a hierarchy of eddy fluctuations where, the larger scale fluctuations enclose smaller scale fluctuations.

2.1   The fundamental gas law for a perfect gas

The root mean square (r.m.s.) circulation speed W over length scale R is related to the corresponding small-scale circulation speed w* and length scale r as

       

      (6)
In the above equation r/R represents the fractional volume intermittency of occurrence of fractal structures (Selvam, 1993) and therefore represents the number of molecules.
       

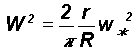
      Therefore

      (7)
and the average kinetic energy of a molecule of mass m is then equal to
       

      (8)
The basic gas equation for a perfect gas based on kinetic theory of gases may now be written as
       

      (9)
which is almost the same as Eq.(1).

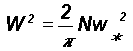
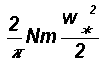
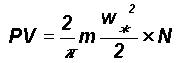
2.2   Distribution of molecular speeds

The steady state upward transport of small-scale fluctuation of speed w* and size scale r in the environment of larger scale fluctuation of speed W and size R is given as
 


(10)

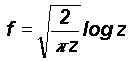
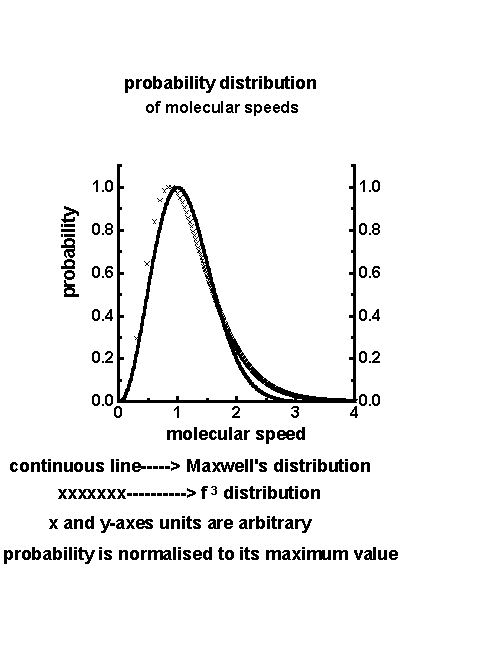
where z is the size scale ratio equal to R/r . Considering three-dimensional fluctuations the fractional contribution (probability density) of smaller length scale r fluctuations in the environment of the larger length scale R fluctuation is given by f 3 . The eddy circulation speeds follow the logarithmic law with respect to the length scale ratio z , namely

(11)

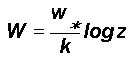
where k is a constant equal to 1/t2 and t is the golden mean equal to (1+Ö 5)/2 (»1.618 ). The eddy circulation speeds are therefore proportional to log z , that is

W » log z

(12)
A graph of f 3 versus log z will give the probability density distribution for molecular speeds. The cell dynamical system model predicted molecular speed distribution in a perfect gas is shown as crosses in Fig.1 (Fig.1). The distributions (Maxwell's and model predicted) are normalised with respect to the maximum speed. There is close agreement between the Maxwell's and model-predicted distributions for molecular speeds in a perfect gas.

3.   Conclusion

The concept of Cantorian fractal spacetime fluctuations is applied to derive the fundamental gas law, namely PV=RT and also the molecular speed distribution for a perfect gas. The model predictions are in agreement with Maxwell's kinetic theory of gases developed in 1859 on probabilistic assumptions.

4.References

Ruhla, C. and G.Barton 1992: The physics of chance Oxford university press, pp.217.

Selvam, A. M., A.S.Ramachandra Murty, G.K.Manohar, S.S.Kandalgaonkar, Bh.V.Ramana Murty 1984a: A new mechanism for the maintenance of fair weather electric field and cloud electrification, Proc. VII International Conference on Atmospheric Electricity, June 3-8, Albany,N.Y.(American Meteorological Society),154-159. http://xxx.lanl.gov/abs/physics/9910006 .

Sikka, P., A.Mary Selvam, A.S.RamachandraMurty, Bh.V.RamanaMurty, 1984: Possible solar influence on atmospheric electric field, Preprint Volume VII International Conference on Atmospheric Electricity, June 3-8, Albany, N.Y., American Meteorological Society, Boston, Mass., USA. http://xxx.lanl.gov/abs/chao-dyn/9806014 .

Selvam, A. M., A.S.Ramachandra Murty and Bh.V. Ramanamurty, 1984b: A New hypothesis for the vertical distribution of atmospheric aerosols, Proc.of the XI Int. Conf. on Atmospheric Aerosols, Condensation and Ice Nuclei, 2-7 Sept., Budapest, Hungary, 77-81. http://xxx.lanl.gov/html/physics/9912014 .

Selvam, A. M. and A.S.R Murty, 1985: Numerical simulation of warm rain process Proc. of the 4th WMO Scientific Conf. on Weather Modification 12-14 August, Honolulu, Hawaii, 503-506. http://xxx.lanl.gov/abs/physics/9911021 .

Selvam A. M., 1988: The dynamics of non-linear effects in optical processes, Journal of Luminescence 40 & 41, 535-536. http://xxx.lanl.gov/abs/chao-dyn/9807005.

Selvam A.M., 1989: A cell dynamical system model for thundercloud electrification, Proc., Int'l . Conf. Lightning and Static Electricity, 26-28 September, University of Bath U.K. http://xxx.lanl.gov/abs/chao-dyn/9809002 .

Selvam, A. M. 1990: Deterministic chaos, fractals and quantum-like mechanics in atmospheric flows,Canadian J.Physics68, 831-841.

Selvam, A. M., J.S.Pethkar and M.K.Kulkarni, 1992: Signatures of a universal spectrum for atmospheric interannual variability in rainfall time series over the Indian region, Int'l J.Climatol.12, 137-152.

Selvam, A. M. 1993: Universal quantification for deterministic chaos in dynamical systems, Applied Mathematical Modelling , 17, 642-649.

Selvam, A. M. and R.R.Joshi, 1995: Universal spectrum for interannual variability in COADS global air and sea surface temperatures, Int'l. J.Climatol. 15, 613 - 623.

Selvam, A. M., J.S. Pethkar, M.K. Kulkarni and R. Vijayakumar, 1996: Signatures of a universal spectrum for atmospheric interannual variability in COADS surface pressure time series, Int'l. J. Climatol. 16, 393 - 404.

Selvam, A.M. 1997: Universal Quantification for Self-Organized Criticality in Atmospheric Flows Proc. Conf. Patterns, Nonlinear Dynamics and Stochastic Behaviour in Spatially Extended Complex Systems, October 24-28, Budapest, Hungary. . http://xxx.lanl.gov/abs/chao-dyn/9710004 .

Fadnavis, S. and A.M.Selvam, 1997: Universal spectrum for interannual variability of rainfall over India and Scotland, Proceedings , National Space Science Symposium, Physical Research Laboratory, Ahmedabad, India, November 25-28. http://xxx.lanl.gov/abs/chao-dyn/9806028 .

Selvam, A.M., 1998: Quasicrystalline pattern formation in fluid substrates and phyllotaxis In Symmetry in Plants, D. Barabe and R.V. Jean (Editors), World Scientific Series in Mathematical Biology and Medicine, Vol.4., Singapore, pp.795-809. http://xxx.lanl.gov/abs/chao-dyn/9806001 .

Selvam, A. M. and S. Fadnavis, 1998: Signatures of a universal spectrum for atmospheric interannual variability in some disparate climatic regimes, Meteorology and Atmospheric Physics, 66, 87-112, (Springer-Verlag, Austria) http://xxx.lanl.gov/abs/chao-dyn/9805028 .

Selvam, A. M. and Suvarna Fadnavis, 1999a: The dynamics of fullerene structure formation : order out of chaos phenomenon, Accepted for publication in FRACTALIA, Romania . http://xxx.lanl.gov/abs/physics/9909052 .

Selvam, A. M., 1999: Cantorian fractal spacetime and quantum-like chaos in neural networks of the human brain, Chaos, Solitons and Fractals 10(1) , 25 - 29 . http://xxx.lanl.gov/abs/chao-dyn/9809003 .

Selvam, A. M., and Suvarna Fadnavis, 1999b: Cantorian fractal spacetime, quantum-like chaos and scale relativity in atmospheric flows, Chaos, Solitons and Fractals 10(9), 1577 - 1582.http://xxx.lanl.gov/abs/chao-dyn/9808015 .

Selvam, A.M. and Suvarna Fadnavis, 1999c: A superstring theory for fractal spacetime, chaos and quantumlike mechanics in atmospheric flows, Chaos, Solitons and Fractals 10(8), 1321-1334. http://xxx.lanl.gov/abs/chao-dyn/9806002 .

Selvam, A. M., D. Sen and S. M. S. Mody, 2000: Critical fluctuations in daily incidence of acute myocardial infarction, Chaos, Solitons and Fractals (Accepted for publication in Chaos, Solitons and Fractals 2000). http://xxx.lanl.gov/abs/chao-dyn/9810017 .

Yavorsky, B. and A.Detlaf, 1975: Handbook of Physics , Mir Publishers, Moscow, pp.965.